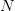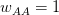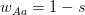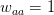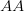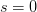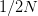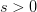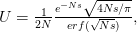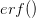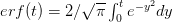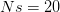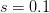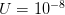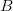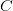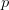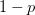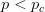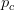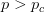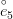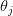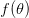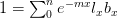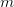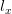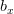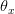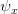Relentless critic of evolutionary psychology, David Buller recently wrote a piece in Scientific American outlining the critique he has developed over the last several years against this particular flavor of human evolutionary studies. The author of Adapting Minds lists four ideas from contemporary evolutionary psychology (EP) that he suggests are fallacious:
- Analysis of Pleistocene Adaptive Problems Yields Clues to the Mind’s Design
- We Know, or Can Discover, Why Distinctively Human Traits Evolved
- “Our Modern Skulls House a Stone Age Mind”
- The Psychological Data Provide Clear Evidence for Pop EP
In my graduate seminar on Evolutionary Theory for the Anthropological Sciences, we read Buller's more technical (2005) critique of EP. I find myself largely in agreement with his criticisms and, importantly, when I disagree with him, I think it is for interesting reasons.
The first of these critiques is, in my opinion, the most far-reaching and damning. The Pleistocene, the geological epoch that lasted from around 1.8 million to 10,000 years before present, takes on the role as a mythical age of creation for EP. You see, the Pleistocene represents out species "Environment of Evolutionary Adaptedness" (EEA), a concept derived from developmental psychology and particularly John Bowlby, the father of attachment theory. In the words of Tooby and Cosmides (1990: 386-387), the EEA "is not a place or a habitat, or even a time period. It is a statistical composite of the adaptation-relevant properties of ancestral environments ecounted by members of ancestral populations, weighted by their frequency and fitness-consequences."
The key question, as Buller notes, is what would such a statistical composite look like for humans? The insight that is regularly trotted out is that humans (hominins really) were everywhere hunter-gatherers until about 10,000 years ago -- and were mostly hunter-gatherers for some substantial period after that! So, what do we know about hunter-gatherers? Much to our collective loss, most of what we know about hunter-gatherers comes from the study of highly marginalized populations. This is because states, with their potential economic surpluses, large populations sizes, and hierarchical social organization (read: efficient militaries) pushed hunter-gatherers into marginal habitats throughout the world as they moved across the landscape. Nonetheless, the hunter-gatherer populations that we know about are a remarkably diverse lot. A terrific reference cataloging some of this diversity is Robert Kelly's (1995) The Foraging Spectrum. In my specific area of interest (i.e., biodemography), Mike Gurven and Hilly Kaplan have recently written a very interesting paper on the diversity of hunter-gatherer patterns of mortality. In this figure, taken from Gurven and Kaplan's paper, we can catch a glimpse of the variability just in hunter-gatherer demography.

Humans are clearly quite different from chimpanzees. The point of Gurven and Kaplan's paper is that the existence of elderly within our societies is not simply an artefact of the modern industrialized world. Old-age is as much a part of the human life cycle as is childhood. Given the long potential lifespans of people in all the sampled populations, there is nonetheless a remarkable diversity in life expectancy (the average number of years lived by a person in the population) portrayed in this figure, considering that these are all groups without access to modern medicine. There are people who live in arid lands of Sub-Saharan Africa (!Kung, Hadza), South American forests (Ache, Tsimane, Yanomamo) and South American grasslands (Hiwi). Life expectancy at age 5, (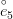 ) varies by as much as 30%. The basic point here is that even in something as basic as age-specific schedules of mortality and fertility, different hunter-gatherer groups are very different from each other (note that the Ache and !Kung differ in their total fertility rates by a factor of nearly two).
) varies by as much as 30%. The basic point here is that even in something as basic as age-specific schedules of mortality and fertility, different hunter-gatherer groups are very different from each other (note that the Ache and !Kung differ in their total fertility rates by a factor of nearly two).
In all likelihood, our Pleistocene ancestors, like the sample of hunter-gatherer societies discussed in Kelly (1995) or Gurven and Kaplan (2007), lived in diverse habitats, engaged in diverse economic activities within the rubric of hunting and gathering, had diverse social structures, met with diverse biotic and abiotic environmental challenges to survival and reproduction, and dealt with diverse hostile and harmonious relations with conspecifics outside of their natal groups or communities. In other words, it's hard to imagine what neat statistical generalizations about hunter-gatherer lifeways -- and the selective forces they entailed -- could emerge from such diversity. People lived in face-to-face societies. People had to integrate disparate sources of information to make decisions about fundamentally uncertain phenomena. There was probably a sexual division of labor, though not necessarily the same one everywhere. There were women and men. Probably some other things too, but not that many. Robert Foley (1996) has a nice critique of what he sees as an extreme simplification of the Pleistocene hunter-gatherer lifeways under the rubric of the EEA.
Another related problem with the EEA line of thinking is this idea that somehow selection stopped when humans developed agriculture. 10,000 years, while brief in the grand scheme of things, is still not exactly evolutionary chump change. That span represents anywhere from 350-450 human generations. This is, in fact, plenty of time for selection to act. We know from genome scans done in the lab of Jonathan Pritchard, for example, that there is extensive evidence for rapid, recent selection in humans. New, complex psychological mechanisms? Probably not, but we should nonetheless not fall into the trap of thinking that somehow evolution stopped for our species 10,000 years ago.
Buller's second fallacy ("We Know, or Can Discover, Why Distinctively Human Traits Evolved") is a deeply difficult problem in human evolution. I'm afraid that my current thinking on this problem leads me to the same pessimistic conclusion that Buller and his colleague Jonathan Kaplan come to: There are just some things that we can't know (scientifically) about human evolution. This arises from the fact that our species is the only member of our genus and we are separated from our sister species by nearly six million years. As Dick Lewontin first noted in 1972, despite our dizzying cultural and social diversity, we are an amazingly homogenous species genetically. I suspect that what this means is that the standard conceit of EP (one that Buller is highly critical of), that humans are everywhere the same critter, is probably true. Unique (and universal) phenomena present science with a particular explanatory challenge. Buller is spot on when he criticizes EP for wanting it both ways. On the one hand, EP sees a robust and universal human nature (an idea to which I am sympathetic, by the way). On the other, EP sees strong selection driving the evolution of diverse psychological mechanisms. The unpleasant reality is that if selection on psychological mechanisms were, in fact, that strong and pervasive, we should expect contemporary heterogeneity in the expression of such adaptations across different populations. This is a topic that University of Illinois anthropological geneticist Charles Roseman and I have talked about quite a bit and have a very slowly gestating manuscript in which we discuss this and other ideas. I know of no convincing evidence that such variation exists and for this and other reasons, I remain a steadfast skeptic of the idea that natural selection has shaped all these important psychological mechanisms independently and with precision to the tasks to which they are supposed to represent engineering solutions.
Buller's argument for fallacy #3 (“Our Modern Skulls House a Stone Age Mind”) is, I think, a little unfair. The major argument he makes on this point is that some of our psychological mechanisms did not, in fact, arise in our Pleistocene hunter-gatherer ancestors, but are of a more ancient, primate (or even mammalian) nature. Honestly, I doubt that this point would elicit many complaints by anyone of the so-called Santa Barbara school. Sometimes critics -- myself included -- make a little too much of the it-all-evolved-in-the-Pleistocene bit. I think this is one example of that. Tooby and Cosmides have themselve argued that the EEA can be thought of as working at a variety of time scales. The emotional systems described by Jaak Panksepp and used by Buller in his critique -- Care, Panic and Play -- are all pretty basic ones for a social species. Indeed, the emotional system of panic almost certainly pre-dates complex sociality. The EEA argument, as laid out by John Tooby and Irv DeVore (1987) and then by Tooby and Cosmides (1990), is essentially one of evolutionary lag: complex adaptations to past environments are carried forward into the present. When a system retains its function, the scale of such lag can be large. Think about bilateral symmetry or the tetrapod bauplan. I think that a fair assessment of Santa Barbara style EP reveals that there is nothing contradictory about the existence of primitive (in the sense of pleisiomorphic) emotional systems in contemporary humans.
Another small point of departure between Buller's critique and my own thinking on the matter is his discussion of David Buss's work on sexual jealousy. Now, I should be perfectly clear here. I happen to think that the whole sex-differences in sexual preferences thing is the most overplayed finding in all of evolutionary science. In class, I refer to this work as Men-Are-From-Mars Evolutionary Psychology. The basic idea is to take whatever tired sexual stereotype that you'd hear in a second rate stand-up comedian's monologue, or read about in airport bookstore self-help tracts and dress it up as the scientifically proven patrimony of our evolutionary past. Ugh. No, the part of Buller's argument with which I disagree is his apparent take on decision-making. Buller writes, "According to Pop EP, many cultural differences stem from a common human nature responding to variable local conditions." I guess I'm not so clear as to what's wrong with such a statement. Isn't that really what he argues in the previous paragraphs when he suggests that women and men have a fundamentally similar reaction to sexual jealousy? On this he writes, "Instead both sexes could have the same evolved capacity to distinguish threatening from nonthreatening infidelities and to experience jealousy to a degree that is proportional to the perceived threat to a relationship in which one has invested mating effort." An evolutionary psychology that took seriously environmental (including cultural) variability and combined it with some preferences over risk and uncertainty and a generalized calculus of costs and benefits: Now that would be interesting! Of course, I'd call that behavioral ecology.
Regarding fallacy #4 ("The Psychological Data Provide Clear Evidence for Pop EP") more generally, I think that Buller is right on. The evidence for many of these so-called psychological adaptations is pretty weak. There is general contempt for population genetics among the smarter (and there are smart ones) evolutionary psychologists with whom I have talked and general ignorance among the less gifted. I think this contempt and/or ignorance is expressed to the detriment of scientific progress in EP. Buller's point that cross-cultural differences are sometimes greater than inter-sexual differences in the psychological traits that are putative adaptations for sex-specific reproductive strategies, while not specifically substantiated, is pretty devastating. This is where population genetics comes in. Thinking about within vs. between population variance is a very important step in understanding the evolutionary forces at work.
The complex organ that is the human brain is certainly the result of selection. As George Williams reminds us, selection is the only evolutionary mechanism that can produce this type of complexity. So, like Buller, I agree that there must be an evolutionary psychology. Our various complaints are with the evolutionary psychology that Buller labels "Pop EP." It's all too easy to be critical. Developing scientific theories for phenomena as complex as those surrounding the evolution of our species is a difficult task and takes ingenuity, courage, and, of course, thick skin. Among the various practitioners of EP of whom Buller is particularly critical, I think that John Tooby and Leda Cosmides are smart people who manifest all these qualities. A fallacy of contemporary discourse -- one that is all too easily seen in anthropological meetings -- is that people who disagree intellectually must hold each other in contempt or otherwise dislike each other. I disagree with much of current EP but I also think there are some interesting ideas among practitioners of EP, once we get beyond the trite Men-Are-From-Mar/Women-Are-From-Venus stereotypes.
Detailing where I think the action is in an interesting evolutionary psychology is at the very least another long blog post. Some areas that I think are promising and/or under-studied include: detailed analyses of cultural transmission dynamics, understanding how people integrate diverse types of information to form decisions with fitness consequences, and understanding how people weigh risk and uncertainty. I have a lot more to say on these topics, so I think it will have to wait for future posts...
References
Buller, D. J. (2005). Evolutionary psychology: the emperor's new paradigm. Trends in Cognitive Sciences, 9(6), 277-283.
Foley, R. (1996). The adaptive legacy of human evolution: A search for the environment of evolutionary adaptedness. Evolutionary Anthropology, 4, 194-203.
Gurven, M., & Kaplan, H. (2007). Longevity Among Hunter-Gatherers: A Cross-Cultural Examination. Population and Development Review, 33(2), 321–365.
Kelly, R. L. (1995). The Foraging Spectrum: Diversity in Hunter-Gatherer Lifeways. Washington DC: Smithsonian Institution Press.
Lewontin, R. C. (1972). The apportionment of human genetic diversity. Evolutionary Biology, 6, 381-398.
Voight, B. F., Kudaravalli, S., Wen, X., & Pritchard, J. K. (2006). A map of recent positive selection in the human genome. PLoS Biology, 4(3), e72. Epub 2006 Mar 2007.
Tooby, J., & Cosmides, L. (1990). The Past Explains the Present - Emotional Adaptations and the Structure of Ancestral Environments. Ethology and Sociobiology, 11(4-5), 375-424.
Tooby, J., & DeVore, I. (1987). The reconstruction of hominid behavioral evolution through strategic modeling. In W. Kinzey (Ed.), Primate Models of Hominid Behavior. Stony Brook: SUNY Press.