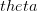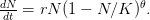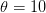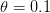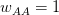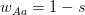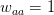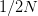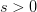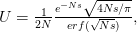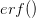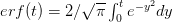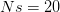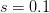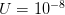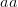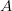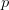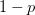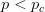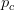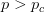I've been traveling all summer while this largest Ebola Virus Disease (EVD) outbreak in recorded history has raged in the West African countries of Guinea, Sierra Leone, Liberia, and (worryingly) Nigeria. My peripatetic state has meant that I haven't been able to devote as much attention to this outbreak as I would like to. There is a great deal of concern -- some might say hysteria -- about EVD and the possibility that it may go pandemic. Tara Smith at least, on her Aetiology blog, has written something sensible, noting that EVD, while terrifying, is controllable with careful public health protective measures, as the historical record from Uganda shows. A recent post by Greg Laden got me to thinking about the numbers from the current EVD outbreak and what we might be able to learn.
EVD was the model disease for the terrible (1995) Dustin Hoffman movie, Outbreak. As we learned in the much more scientifically-accurate (2011) movie Contagion (which is based on an equally terrifying aerosolized Nipah virus), one of the key pieces of information regarding an epidemic is the basic reproduction number, 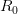 . The basic reproduction number tells us how many secondary infections are expected (i.e., on average) to be produced by a single, typical case at the outset of an epidemic before the pool of susceptible people has been depleted.
. The basic reproduction number tells us how many secondary infections are expected (i.e., on average) to be produced by a single, typical case at the outset of an epidemic before the pool of susceptible people has been depleted. 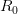 provides lots of information about epidemics, including: (1) the epidemic threshold (i.e., whether or not an epidemic will occur, which happens in the deterministic case when
provides lots of information about epidemics, including: (1) the epidemic threshold (i.e., whether or not an epidemic will occur, which happens in the deterministic case when 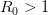 ), (2) the initial rate of increase of an epidemic, (3) the critical vaccination threshold (i.e., what fraction of the population you need to vaccinate to prevent an outbreak), (4) the endemic equilibrium of an infection (i.e., the fraction of the population that is infected in between outbreaks), and (5) the final size of the epidemic (i.e., the fraction of the total population that is ever infected when the epidemic is over).
), (2) the initial rate of increase of an epidemic, (3) the critical vaccination threshold (i.e., what fraction of the population you need to vaccinate to prevent an outbreak), (4) the endemic equilibrium of an infection (i.e., the fraction of the population that is infected in between outbreaks), and (5) the final size of the epidemic (i.e., the fraction of the total population that is ever infected when the epidemic is over).
Thus, for a novel outbreak, it's good to have an idea of 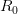 . I've been a bit out of the loop this summer and haven't seen any estimates so I figured that I would see what I could do. I fully realize that someone may have already done this and that I am not yet aware of it. I also recognize that, if someone has done this, they've probably done it better. This is a blog, not a peer-reviewed paper, and I am away from my usual resources, so please take this in the back-of-the-envelope spirit in which it is intended. I reserve the right to retract, etc. I will also post the R code that I used to make the calculations. I hope that this may prove helpful to others interested in the dynamics of outbreaks.
. I've been a bit out of the loop this summer and haven't seen any estimates so I figured that I would see what I could do. I fully realize that someone may have already done this and that I am not yet aware of it. I also recognize that, if someone has done this, they've probably done it better. This is a blog, not a peer-reviewed paper, and I am away from my usual resources, so please take this in the back-of-the-envelope spirit in which it is intended. I reserve the right to retract, etc. I will also post the R code that I used to make the calculations. I hope that this may prove helpful to others interested in the dynamics of outbreaks.
In their terrific (2003) paper on the SARS outbreak, Marc Lipsitch and colleagues provided a method for estimating the reproduction number from outbreak data. Note that this is a more generalized reproduction number, which we call 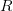 , than is the basic reproduction number,
, than is the basic reproduction number, 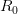 . The key difference is that a reproduction number can be calculated at any point in an outbreak, whereas
. The key difference is that a reproduction number can be calculated at any point in an outbreak, whereas 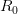 is only technically correct at the outset (the zero index in
is only technically correct at the outset (the zero index in 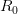 indicates the "generation" of the outbreak where "0" refers to the index case, a.k.a., "patient zero"). I've simply used the count of total cases from this week. It is straightforward to extend the calculation to previous counts. I haven't yet had a chance to do this because there is no convenient collection of data that I can find with my current access constraints.
indicates the "generation" of the outbreak where "0" refers to the index case, a.k.a., "patient zero"). I've simply used the count of total cases from this week. It is straightforward to extend the calculation to previous counts. I haven't yet had a chance to do this because there is no convenient collection of data that I can find with my current access constraints.
The method involves equating 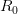 for a simplified SEIR system to the observed rate of increase of the outbreak at some point in time
for a simplified SEIR system to the observed rate of increase of the outbreak at some point in time 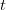 , using the fact that the reproduction number is approximately equivalent to the growth rate of the epidemic. See the supplementary information from Lipsitch et al. (2003) for details of the method. In brief, we calculate the dominant eigenvalue of the linearized SEIR model, for which it is straightforward to write an analytical formula, and equate this to
, using the fact that the reproduction number is approximately equivalent to the growth rate of the epidemic. See the supplementary information from Lipsitch et al. (2003) for details of the method. In brief, we calculate the dominant eigenvalue of the linearized SEIR model, for which it is straightforward to write an analytical formula, and equate this to ![log[Y(t)]/t](http://monkeysuncle.stanford.edu/wp-content/plugins/latex/cache/tex_380b1cea9aadb2220e7ff6b252ec1556.gif) , the empirical growth rate of the epidemic (where
, the empirical growth rate of the epidemic (where 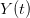 is the cumulative number of cases at time
is the cumulative number of cases at time 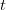 ). Lipsitch et al. (2003) note that using the standard formula for the characteristic equation of the eigenvalues of the linearized SEIR model, we can solve for the reproduction number as:
). Lipsitch et al. (2003) note that using the standard formula for the characteristic equation of the eigenvalues of the linearized SEIR model, we can solve for the reproduction number as:
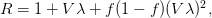
where 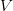 is the serial interval (i.e., the summed duration of the incubation period,
is the serial interval (i.e., the summed duration of the incubation period, 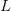 , and the duration of the infectious period,
, and the duration of the infectious period, 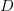 ),
), 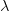 is the positive root of the characteristic equation which we set equal to
is the positive root of the characteristic equation which we set equal to ![\log[Y(t)]/t](http://monkeysuncle.stanford.edu/wp-content/plugins/latex/cache/tex_60ed99c4631e6be2f173613ae73e67f9.gif) , and
, and 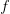 is the ratio of the infectious period of the serial interval.
is the ratio of the infectious period of the serial interval.
I got the case data from the weekly WHO outbreak report for 11 August 2014. For this week 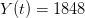 . For the start time of the epidemic in the currently afflicted countries, I used the date of 10 March 2014, taken from this week's NEJM paper by Blaize et al. (2014). For the serial interval data, I used the values provided by the Legrand et al. (2007). Because Legrand et al. (2007) provide mean values of the relevant parameters -- and this is a different epidemic -- I used a variety of values for
. For the start time of the epidemic in the currently afflicted countries, I used the date of 10 March 2014, taken from this week's NEJM paper by Blaize et al. (2014). For the serial interval data, I used the values provided by the Legrand et al. (2007). Because Legrand et al. (2007) provide mean values of the relevant parameters -- and this is a different epidemic -- I used a variety of values for 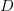 and
and 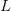 to calculate
to calculate 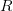 . It turns out that it doesn't matter all that much; the estimates of
. It turns out that it doesn't matter all that much; the estimates of 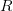 are pretty stable.
are pretty stable.
I plot the values of 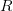 against the duration of the latent period. The different lines are for the different values of the duration of infectiousness.
against the duration of the latent period. The different lines are for the different values of the duration of infectiousness. 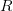 increases with both. What we see is that at this point in the epidemic at least,
increases with both. What we see is that at this point in the epidemic at least, 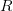 ranges from around 1.3 to 2.6, depending on specifics of the course of the disease. This is not all that high -- about the same as various flavors of influenza and considerably less than, say, pertussis. This is good news for potential control, if we could just rally some more international support for control of this serious infection...
ranges from around 1.3 to 2.6, depending on specifics of the course of the disease. This is not all that high -- about the same as various flavors of influenza and considerably less than, say, pertussis. This is good news for potential control, if we could just rally some more international support for control of this serious infection...
Here is the R code for doing the calculations and creating this figure:
[r]
library(lubridate)
# number of cases as of 11 August 2014
# http://www.who.int/csr/don/2014_08_11_ebola/en/
cases <- 1848
# start of epidemic in Guinea: 10 March 2014
# Blaize et al. (2014), NEJM. DOI: 10.1056/NEJMoa1404505
s <- dmy("10-03-14")
e <- dmy("11-08-14")
t <- e-s
# Time difference of 154 days
## incubation period 2-21 days
## http://www.who.int/mediacentre/factsheets/fs103/en/
## duration of infectiousness: virus detected in of lab-infected man 61 days!
## Legrande et al. (2007) use L=7 and D=10
## doi:10.1017/S0950268806007217
lambda <- log(cases)/t
## From Lipsitch et al. (2003)
## lambda is the dominant eigenvalue of the linearized SEIR model
## V is the serial interval V = D + L
## D is duration infectious period, L is duration of latent period
## f is the ratio of the the infectious period to the serial interval
## to solve for R set the eigenvalue equal to the observed exponential growth rate of the epidemic log(Y(t))/t
Rapprox <- function(lambda,V,f) 1 + V*lambda + f*(1-f)*(V* lambda)^2
RR <- matrix(0, nr=10, nc=10)
L <- seq(3,12)
D <- seq(5,14)
for(i in 1:length(L)){
for(j in 1:length(D)){
RR[i,j] <- Rapprox(lambda,L[i]+D[j],D[j]/(L[i]+D[j]))
}
}
cols <- topo.colors(10)
png(file="Ebola-R0-plot1.png")
plot(L, RR[1,], type="n", xlab="Duration of Incubation", ylab="Reproduction Number",ylim=c(1,2.5))
for(i in 1:10) lines(L, RR[i,], lwd=2, col=cols[i])
dev.off()
[/r]