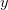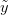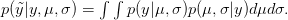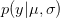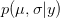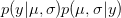Category Archives: Statistics

science, Statistics

Thoughts on Black Swans and Antifragility

2 Comments

I have recently read the latest book by Nassim Nicholas Taleb, Antifragile. I read his famous The Black Swan a while back while in the field and wrote lots of notes. I never got around to posting those notes since they were quite telegraphic (and often not even electronic!), as they were written in the middle of the night while fighting insomnia under mosquito netting. The publication of his latest, along with the time afforded by my holiday displacement, gives me an excuse to formalize some of these notes here. Like Andy Gelman, I have so many things to say about this work on so many different topics, this will be a bit of a brain dump.

Taleb's work is quite important for my thinking on risk management and human evolution so it is with great interest that I read both books. Nonetheless, I find his works maddening to say the least. Before presenting my critique, however, I will pay the author as big a compliment as I suppose can be made. He makes me think. He makes me think a lot, and I think that there are some extremely important ideas is his writings. From my rather unsystematic readings of other commentators, this seems to be a pretty common conclusion about his work. For example, Brown (2007) writes in The American Statistician, "I predict that you will disagree with much of what you read, but you'll be smarter for having read it. And there is more to agree with than disagree. Whether you love it or hate it, it’s likely to change public attitudes, so you can't ignore it." The problem is that I am so distracted by all the maddening bits that I regularly nearly miss the ideas, and it is the ideas that are important. There is so much ego and so little discipline on display in his books, The Black Swan and Antifragile.

Some of these sentiments have been captured in Michiko Kakutani's excellent review of Antifragile. There are some even more hilarious sentiments communicated in Tom Bartlett's non-profile in the Chronicle of Higher Education.

I suspect that if Taleb and I ever sat down over a bottle of wine, we would not only have much to discuss but we would find that we are annoyed -- frequently to the point of apoplexy -- by the same people. Nonetheless, I find one of the most frustrating things about reading his work the absurd stereotypes he deploys and broad generalizations he uses to dismiss the work of just about any academic researcher. His disdain for academic research interferes with his ability to make cogent critique. Perhaps I have spent too much time at Stanford, where the nerd is glorified, but, among other things, I find his pejorative use of the term "nerd" for people like Dr. John, as contrasted to man-of-his-wits Stereotyped, I mean, Fat Tony off-putting and rather behind the times. Gone are the days when being labeled a nerd is a devastating put down.

My reading of Taleb's critiques of prediction and risk management is that the primary problem is hubris. Is there anything fundamentally wrong with risk assessment? I am not convinced there is, and there are quite likely substantial benefits to systematic inquiry. The problem is that the risk assessment models become reified into a kind of reality. I warn students – and try to regularly remind myself – never to fall in love with one's own model. Something that many economists and risk modelers do is start to believe that their models are something more real than heuristic. George Box's adage has become a bit cliche but nonetheless always bears repeating: all models are wrong, but some are useful. We need to bear in mind the wrongness of models without dismissing their usefulness.

One problem about both projection and risk analysis, that Taleb does not discuss, is that risk modelers, demographers, climate scientists, economists, etc. are constrained politically in their assessments. The unfortunate reality is that no one wants to hear how bad things can get and modelers get substantial push-back from various stakeholders when they try to account for real worst-case scenarios.

There are ways of building in more extreme events than have been observed historically (Westfall and Hilbe (2007), e.g., note the use of extreme-value modeling). I have written before about the ideas of Martin Weitzman in modeling the disutility of catastrophic climate change. While he may be a professor at Harvard, my sense is that his ideas on modeling the risks of catastrophic climate change are not exactly mainstream. There is the very tangible evidence that no one is rushing out to mitigate the risks of climate change despite the fact that Weitzman's model makes it pretty clear that it would be prudent to do so. Weitzman uses a Bayesian approach which, as noted by Westfall and Hilbe, is a part of modern statistical reasoning that was missed by Taleb. While beyond the scope of this already hydra-esque post, briefly, Bayesian reasoning allows one to combine empirical observations with prior expectations based on theory, prior research, or scenario-building exercises. The outcome of a Bayesian analysis is a compromise between the observed data and prior expectations. By placing non-zero probability on extreme outcomes, a prior distribution allows one to incorporate some sense of a black swan into expected (dis)utility calculations.

Nor does the existence of black swans mean that planning is useless. By their very definition, black swans are rare -- though highly consequential -- events. Does it not make sense to have a plan for dealing with the 99% of the time when we are not experiencing a black swan event? To be certain, this planning should not interfere with our ability to respond to major events but I don't see any evidence that planning for more-or-less likely outcomes necessarily trades-off with responding to unlikely outcomes.

Taleb is disdainful about explanations for why the bubonic plague didn't kill more people: "People will supply quantities of cosmetic explanations involving theories about the intensity of the plague and 'scientific models' of epidemics." (Black Swan, p. 120) Does he not understand that epidemic models are a variety of that lionized category of nonlinear processes he waxes about? He should know better. Epidemic models are not one of these false bell-curve models he so despises. Anyone who thinks hard about an epidemic process -- in which an infectious individual must come in contact with a susceptible one in order for a transmission event to take place -- should be able to infer that an epidemic can not infect everyone. Epidemic models work and make useful predictions. We should, naturally, exhibit a healthy skepticism about them as we should any model. But they are an important tool for understanding and even planning.

Indeed, our understanding gained from the study of (nonlinear) epidemic models has provided us with the most powerful tools we have for control and even eradication. As Hans Heesterbeek has noted, the idea that we could control malaria by targeting the mosquito vector of the disease is one that was considered ludicrous before Ross's development of the first epidemic model. The logic was essentially that there are so many mosquitoes that it would be absurdly impractical to eliminate them all. But the Ross model revealed that epidemics -- because of their nonlinearity -- have thresholds. We don't have to eliminate all the mosquitoes to break the malaria transmission cycle; we just need to eliminate enough to bring the system below the epidemic threshold. This was a powerful idea and it is central to contemporary public health. It is what allowed epidemiologists and public health officials to eliminate smallpox and it is what is allowing us to very nearly eliminate polio if political forces (black swans?) will permit.

Taleb's ludic fallacy (i.e., games of chance are somehow an adequate model of randomness in the world) is great. Quite possibly the most interesting and illuminating section of The Black Swan happens on p. 130 where he illustrates the major risks faced by a casino. Empirical data make a much stronger argument than do snide stereotypes. This said, Lund (2007) makes the important point that we need to ask what exactly is being modeled in any risk assessment or projection. One of the most valuable outcomes of any formalized risk assessment (or formal model construction more generally) is that it forces the investigator to be very explicit about what is being modeled. The output of the model is often of secondary importance.

Much of the evidence deployed in his books is what Herb Gintis has called "stylized facts" and, of course, is subject to Taleb's own critique of "hidden evidence." Because the stylized facts are presented anecdotally, there is no way to judge what is being left out. A fair rejoinder to this critique might be that these are trade publications meant for a mass market and are therefore not going to be rich in data regardless. However, the tone of the books – ripping on economists and bankers but also statisticians, historians, neuroscientists, and any number of other professionals who have the audacity to make a prediction or provide a causal explanation – makes the need for more measured empirical claims more important. I suspect that many of these people actually believe things that are quite compatible with the conclusions of both The Black Swan and Antifragile.

On Stress

The notion of antifragility turns on systems getting stronger when exposed to stressors. But we know that not all stressors are created equally. This is where the work of Robert Sapolsky really comes into play. In his book Why Zebras Don't Get Ulcers, Sapolsky, citing the foundational work of Hans Seyle, notes that some stressors certainly make the organism stronger. Certain types of stress ("good stress") improves the state of the organism, making it more resistant to subsequent stressors. Rising to a physical or intellectual challenge, meeting a deadline, competing in an athletic competition, working out: these are examples of good stresses. They train body, mind, and emotions and improve the state of the individual. It is not difficult to imagine that there could be similar types of good stressors at levels of organization higher than the individual too. The way the United States came together as a society to rise to the challenge of World War II and emerge as the world's preeminent industrial power comes to mind. An important commonality of these good stressors is the time scale over which they act. They are all acute stressors that allow recovery and therefore permit the subsequently improved performance.

However, as Sapolsky argues so nicely, when stress becomes chronic, it is no longer good for the organism. The same glucocorticoids (i.e., "stress hormones") that liberate glucose and focus attention during an acute crisis induce fatigue, exhaustion, and chronic disease when the are secreted at high levels chronically.

Any coherent theory of antifragility will need to deal with the types of stress to which systems are resistant and, importantly, have a strengthening effect. Using the idea of hormesis – that a positive biological outcome can arise from taking low doses of toxins – is scientifically hokey and boarders on mysticism. It unfortunately detracts from the good ideas buried in Antifragile.

I think that Taleb is on to something with the notion of antifragility but I worry that the policy implications end up being just so much orthodox laissez-faire conservatism. There is the idea that interventions – presumably by the State – can do nothing but make systems more fragile and generally worse. One area where the evidence very convincingly suggests that intervention works is public health. Life expectancy has doubled in the rich countries of the developed world from the beginning of the twentieth century to today. Many of the gains were made before the sort of dramatic things that come to mind when many people think about modern medicine. It turns out that sanitation and clean water went an awful long way toward decreasing mortality well before we had antibiotics or MRIs. Have these interventions made us more fragile? I don't think so. The jury is still out, but it seems that reducing the infectious disease burden early in life (as improved sanitation does) seems to have synergistic effects on later-life mortality, an effect is mediated by inflammation.

On The Academy

Taleb drips derision throughout his work on university researchers. There is a lot to criticize in the contemporary university, however, as with so many other external critics of the university, I think that Taleb misses essential features and his criticisms end up being off base. Echoing one of the standard talking points of right-wing critics, Taleb belittles university researchers as being writers rather than doers (echoing the H.L. Menken witticism  "Those who can do; those who can't teach"). Skin in the game purifies thought and action, a point with which I actually agree, however, thinking that that university researchers live in a world lacking consequences is nonsense. Writing is skin in the game. Because we live in a quite free society – and because of important institutional protections on intellectual freedom like tenure (another popular point of criticism from the right) – it is easy to forget that expressing opinions – especially when one speaks truth to power – can be dangerous. Literally. Note that intellectuals are often the first ones to go to the gallows when there are revolutions from both the right and the left: Nazis, Bolsheviks, and Mao's Cultural Revolution to name a few. I occasionally get, for lack of a better term, unbalanced letters from people who are offended by the study of evolution and I know that some of my colleagues get this a lot more than I. Intellectuals get regular hate mail, a phenomenon amplified by the ubiquity of electronic communication. Writers receive death threats for their ideas (think Salman Rushdie). Ideas are dangerous and communicating them publicly is not always easy, comfortable, or even safe, yet it is the professional obligation of the academic.

There are more prosaic risks that academics face that suggest to me that they do indeed have substantial skin in the game. There is a tendency for critics from outside the academy to see universities as ossified places where people who "can't do" go to live out their lives. However, the university is a dynamic place. Professors do not emerge fully formed from the ivory tower. They must be trained and promoted. This is the most obvious and ubiquitous way that what academics write has "real world" consequences – i.e., for themselves. If peers don't like your work, you won't get tenure. One particularly strident critic can sink a tenure case. Both the trader and the assistant professor have skin in their respective games – their continued livelihoods depend upon their trading decisions and their writing. That's pretty real. By the way, it is a huge sunk investment that is being risked when an assistant professor comes up for tenure. Not much fun to be forty and let go from your first "real" job since you graduated with your terminal degree... (I should note that there are problems with this – it can lead to particularly conservative scholarship by junior faculty, among other things, but this is a topic for its own post.)

Now, I certainly think that are more and less consequential things to write about. I have gotten more interested in applied problems in health and the environment as I've moved through my career because I think that these are important topics about which I have potentially important things to say (and, yes, do). However, I also think it is of utmost importance to promote the free flow of ideas, whether or not they have obvious applications. Instrumentally, the ability to pursue ideas freely is what trains people to solve the sort of unknown and unforecastable problems that Taleb discusses in The Black Swan. One never knows what will be relevant and playing with ideas (in the personally and professionally consequential world of the academy) is a type of stress that makes academics better at playing with ideas and solving problems.

One of the major policy suggestions of Atifragile is that tinkering with complex systems will be superior to top-down management. I am largely sympathetic to this idea and to the idea that high-frequency-of-failure tinkering is also the source of innovation. Taleb contrasts this idea of tinkering is "top-down" or "directed" research, which he argues regularly fails to produce innovations or solutions to important problems. This notion of "top-down," "directed" research is among the worst of his various straw men and a fundamental misunderstanding of the way that science works. A scientist writes a grant with specific scientific questions in mind, but the real benefit of a funded research program is the unexpected results one discovers while pursuing the directed goals. As a simple example, my colleague Tony Goldberg has discovered two novel simian hemorrhagic viruses in the red colobus monkeys of western Uganda as a result of our big grant to study the transmission dynamics and spillover potential of primate retroviruses. In the grant proposal, we discussed studying SIV, SFV, and STLV. We didn't discuss the simian hemorrhagic fever viruses because we didn't know they existed! That's what discovery means. Their not being explicitly in the grant didn't stop Tony and his collaborators from the Wisconsin Regional Primate Center from discovering these viruses but the systematic research meant that they were in a position to discover them.

The recommendation of adaptive, decentralized tinkering in complex systems is in keeping with work in resilience (another area about which Taleb is scornful because it is the poor step-child of antifragility). Because of the difficulty of making long-range predictions that arises from nonlinear, coupled systems, adaptive management is the best option for dealing with complex environmental problems. I have written about this before here.

So, there is a lot that is good in the works of Taleb. He makes you think, even if spend a lot of time rolling your eyes at the trite stereotypes and stylized facts that make up much of the rhetoric of his books. Importantly, he draws attention to probabilistic thinking for a general audience. Too much popular communication of science trades in false certainties and the mega-success of The Black Swan in particular has done a great service to increasing awareness among decision-makers and the reading public about the centrality of uncertainty. Antifragility is an interesting idea though not as broadly applicable as Taleb seems to think it is. The inspiration for antifragility seem to lie in largely biological systems. Unfortunately, basing an argument on general principles drawn from physiology, ecology, and evolutionary biology pushes Taleb's knowledge base a bit beyond its limit. Too often, the analogies in this book fall flat or are simply on shaky ground empirically. Nonetheless, recommendations for adaptive management and bricolage are sensible for promoting resilient systems and innovation. Thinking about the world as an evolving complex system rather than the result of some engineering design is important and if throwing his intellectual cachet behind this notion helps it to get as ingrained into the general consciousness as the idea of a black swan has become, then Taleb has done another major service.

science, Statistics

The Igon Value Problem

1 Comment

Priceless. Steve Pinker wrote a spectacular review of Malcolm Gladwell's latest book, What the Dog Saw and Other Adventures, in the New York Times today. I regularly read and enjoy Gladwell's essays in the New Yorker, but I find his style sometimes problematic, verging on anti-intellectual, and I'm thrilled to see a scientist of Pinker's stature calling him out.

Pinker coins a term for the problem with Gladwell's latest book and his work more generally.  Pinker's term: "The Igon Value Problem" is a clever play on the Eigenvalue Problem in mathematics.  You see, Gladwell apparently quotes someone referring to an "igon value." This is clearly a concept he never dealt with himself even though it is a ubiquitous tool in the statistics and decision science about which Gladwell is frequently so critical.  According to Pinker, the Igon Value Problem occurs "when a writer’s education on a topic consists in interviewing an expert," leading him or her to offering "generalizations that are banal, obtuse or flat wrong."  In other words, the Igon Value Problem is one of dilettantism.  Now, this is clearly a constant concern for any science writer, who has the unenviable task of rendering extremely complex and frequently quite technical information down to something that is simultaneously accurate, understandable, and interesting. However, when the bread and butter of one's work involves criticizing scientific orthodoxy, it seems like one needs to be extremely vigilant to get the scientific orthodoxy right.

Pinker raises the extremely important point that the decisions we make using the formal tools of decision science (and cognate fields) represent solutions to the inevitable trade-offs between information and cost.  This cost can take the form of financial cost, time spent on the problem, or computational resources, to name a few. Pinker writes:

Improving the ability of your detection technology to discriminate signals from noise is always a good thing, because it lowers the chance you’ll mistake a target for a distractor or vice versa. But given the technology you have, there is an optimal threshold for a decision, which depends on the relative costs of missing a target and issuing a false alarm. By failing to identify this trade-off, Gladwell bamboozles his readers with pseudoparadoxes about the limitations of pictures and the downside of precise information.

Pinker is particularly critical of an analogy Gladwell draws in one of his essays between predicting the success of future teachers and future professional quarterbacks.  Both are difficult decision tasks fraught with uncertainty.  Predicting whether an individual will be a quality teacher based on his or her performance on standardized tests or the presence or absence of teaching credentials is an imperfect process just as predicting the success of a quarterback in the N.F.L. based on his performance at the collegiate level.  Gladwell argues that anyone with a college degree should be allowed to teach and that the determination of the qualification for the job beyond the college degree should only be made after they have taught. This solution, he argues, is better than the standard practice of  credentialing, evaluating, and "going back and looking for better predictors.” You know, science? Pinker doesn't hold back in his evaluation of this logic:

But this “solution” misses the whole point of assessment, which is not clairvoyance but cost-effectiveness. To hire teachers indiscriminately and judge them on the job is an example of “going back and looking for better predictors”: the first year of a career is being used to predict the remainder. It’s simply the predictor that’s most expensive (in dollars and poorly taught students) along the accuracy- cost trade-off. Nor does the absurdity of this solution for professional athletics (should every college quarterback play in the N.F.L.?) give Gladwell doubts about his misleading analogy between hiring teachers (where the goal is to weed out the bottom 15 percent) and drafting quarterbacks (where the goal is to discover the sliver of a percentage point at the top).

This evaluation is spot-on. As a bit of an aside, the discussion of predicting the quality of prospective quarterbacks also reminds me of one of the great masterpieces of statistical science and the approach described by this paper certainly has a bearing on the types of predictive problems of which Gladwell ruminates.  In a 1975 paper, Brad Efron and Carl Morris present a method for predicting 18 major league baseball players' 1970 season batting average based on their first 45 at-bats. The naïve method for predicting (no doubt, the approach Gladwell's straw "we" would take) is simply to use the average after the first 45 at-bats. Turns out, there is a better way to solve the problem, in the sense that you can make more precise predictions (though hardly clairvoyant).  The method turns on what a Bayesian would call "exchangeability."  Basically, the idea is that being a major league baseball player buys you a certain base prediction for the batting average.  So if we combine the averages across the 18 players and with each individual's average in a weighted manner, we can make a prediction that has less variation in it.  A player's average after a small number of at-bats is a reflection of his abilities but also lots of forces that are out of his control -- i.e., are due to chance.  Thus, the uncertainty we have in a player's batting based on this small record is partly due to the inherent variability in his performance but also due to sampling error.  By pooling across players, we combine strength and remove some of this sampling error, allowing us to make more precise predictions. This approach is lucidly discussed in great detail in my colleague Simon Jackman's new book, draft chapters of which we used when we taught our course on Bayesian statistical methods for the social sciences.

Teacher training and credentialing can be thought of as strategies for ensuring exchangability in teachers, aiding the prediction of teacher performance.  I am not an expert, but it seems like we have a long way to go before we can make good predictions about who will become an effective teacher and who will not.  This doesn't mean that we should stop trying.

Janet Maslin, in her review of What the Dog Saw, waxes about Gladwell's scientific approach to his essays. She writes that the dispassionate tone of his essays "tames visceral events by approaching them scientifically." I fear that this sentiment, like the statements made in so many Gladwell works, reflects the great gulf between most educated Americans and the realities of scientific practice (we won't even talk about the gulf between less educated Americans and science).  Science is actually a passionate, messy endeavor and sometimes we really do get better by going back and finding better predictors.

Human Ecology, Statistics

Fold Catastrophe Model

4 Comments

My last post, which I had to cut short, discussed the recent paper by Scheffer et al. (2009) on the early warning signs of impending catastrophe. This paper encapsulates a number of things that I think are very important and relate to some current research (and teaching interests). Scheffer and colleagues show the consequences on time series of state observations when a dynamical system characterized by a fold bifurcation is forced across its attractor where parts of this attractor are stable and others are unstable.  In my last post, I described the fold catastrophe model as an attractor that looks like an "sideways N." I just wanted to briefly unpack that statement.  First, an attractor is kind of like an equilibrium.  It's a set of points to which a dynamical system evolves.  When the system is perturbed, it tends to return to an attractor.  Attractors can be fixed points or cycles or extremely complex shapes, depending upon the particulars of the system.

The fold catastrophe model posits an attractor that looks like this figure, which I have more or less re-created from Scheffer et al. (2009), Box 1.

foldThe solid parts of the curve are stable -- when the system state is perturbed when in the vicinity of this part of the attractor, it tends to return, as indicated by the grey arrows pointing back to the attractor.  The dashed part of the attractor is unstable -- perturbations in this neighborhood tend to move away from the attractor.  This graphical representation of the system makes it pretty easy to see how a small perturbation could dramatically change the system if the current combination of conditions and system state place the system on the attractor near the neighborhood where the attractor changes from stable to unstable.  The figure illustrates one such scenario.  The conditions/system state start at point F1. A small forcing perturbs the system off this point across the bifurcation.  Further forcing now moves the system way off the current state to some new, far away, stable state.  We go from a very high value of the system state to a very low value with only a very small change in conditions.  Indeed, in this figure, the conditions remain constant from point F1 to the new value indicated by the white point -- just a brief perturbation was sufficient to cause the drastic change.  I guess this is part of the definition of a catastrophe.

The real question in my mind, and one that others have asked, is how relevant is the fold catastrophe model for real systems?  This is something I'm going to have to think about. One thing that is certain is that this is a pedagogically very useful approach as it makes you think... and worry.

Statistics

Predicting Catastrophe?

2 Comments

There is an extremely cool paper in this week's Nature by Scheffer and colleagues. I'm too busy right now to write much about it, but I wanted to mention it, even if only briefly.  The thing that I find so remarkable about this paper is that it's really not the sort of thing that I usually like.  The paper essentially argues that there are certain generic features of many systems as they move toward catastrophic change.  The paper discusses epileptic seizures, asthma attacks, market collapses, abrupt shifts in oceanic circulation and climate, and ecological catastrophes such as sudden shifts in rangelands, or crashes of fish or wildlife populations. At first, it sounds like the vaguely mystical ideas about transcendent complexity, financial physics, etc.  But really, there are a number of very sensible observations about dynamical systems and a convincing argument that these features will be commonly seen in real complex systems.

The basic idea is that there are a number of harbingers of catastrophic change in time series of certain complex systems.  The model the authors use is the fold catastrophe model, where there is an attractor that folds back on itself like a sideways "N".  As one gets close to a catastrophic bifurcation, a very straightforward analysis shows that the rate of return to the attractor decreases (I have some notes that describe the stability of the equilibria of simple population models here. The tools discussed in Scheffer et al. (2009) are really just generalizations of these methods).  As the authors note, one rarely has the luxury of measuring rates of return to equilibria in real systems but, fortunately, there are relatively easily measured consequences of this slow-down of rates of return to the attractor. They show in what I think is an especially lucid manner how the correlations between consecutive observations in a time series will increase as one approaches one of these catastrophic bifurcation points. This increased correlation has the effect of increasing the variance.

So, two ways to diagnose an impending catastrophe in a system that is characterized by the fold bifurcation model are: (1) an increase in variance of the observations in the series and (2) an increase in the lag-1 autocorrelation.  A third feature of impending catastrophes does not have quite as intuitive an explanation (at least for me), but is also relatively straightforward.  Dynamical systems approaching a catastrophic bifurcation will exhibit increased skewness to the fluctuations as well as flickering.  The skewness means that the distribution of period-to-period fluctuations will become increasingly asymmetric.  This has to do with the shape of the underlying attractor and how the values of the system are forced across it. Flickering means that the values will bounce back and forth between two different regimes (say, high and low) rapidly for a period before the catastrophe.  This happens when the system is being forced with sufficient strength that it is bounced between two basins of attraction before getting sucked into a new one for good (or at least a long time).

In summary, there are four generic indicators of impending catastrophe in the fold bifurcation model:

  1. Increased variance in the series
  2. Increased autocorrelation
  3. Increased skewness in the distribution of fluctuations
  4. Flickering between two states

There are all sorts of worrisome implications in these types of models for climate change, production systems, disease ecology, and the dynamics of endangered species.  What I hope is that by really getting a handle on these generic systems, we will develop tools that will help us identify catastrophes soon enough that we might actually be able to do something about some of them.  The real challenge, of course, is developing tools that give us the political will to tackle serious problems subject to structural uncertainty. I won't hold my breath...

Demography, Evolution, Human Ecology, Statistics

Stanford Workshop in Biodemography

3 Comments

On 29-31 October, we will be holding our next installment of the Stanford Workshops in Formal Demography and Biodemography, the result of an ongoing grant from NICHD to Shripad Tuljapurkar and myself.  This time around, we will venture onto the bleeding edge of biodemography.  Specific topics that we will cover include:

  • The use of genomic information on population samples
  • How demographers and biologists use longitudinal data
  • The use of quantitative genetic approaches to study demographic questions
  • How demographers and biologists model life histories

Information on the workshop, including information on how to apply for the workshop and a tentative schedule, can be found on the IRiSS website. We've got an incredible line-up of international scholars in demography, ecology, evolutionary biology, and genetics coming to give research presentations.

The workshop is intended for advanced graduate students (particularly students associated with NICHD-supported Population Centers), post-docs, and junior faculty who want to learn about the synergies between ecology, evolutionary biology, and demography. Get your applications in soon -- these things fill up fast!

Demography, R, Statistics

Why Use R?

4 Comments

An anthropologist colleague who did a post-doc in a population center has been trying to get a group of people at his university together to think about population issues.  This is something I'm all for and am happy to help in whatever little way I can to facilitate especially anthropologists developing their expertise in demography.  One of the activities they have planned for this population interest group is a workshop on the R statistical programming language. The other day he wrote me with the following very reasonable question that has been put to him by several of the people in his group: Sure R is free but other than that why should someone bother to learn new software when there is perfectly acceptable commercial software out there?  This question is particularly relevant when one works for an institution like a university where there are typically site licenses and other mechanisms for subsidizing the expense of commercial software (which can be substantial).  What follows is, more or less, what I said to him.

I should start out by saying that there is a lot to be said for free. I pay several hundred dollars a year for commercial software that I don't actually use that often. Now, when I need it, it's certainly nice to know it's there but if I didn't have a research account paying for this software, I might let at least one or two of these licenses slide.  I very occasionally use Stata because the R package that does generalized linear mixed models has had a bug in the routine that fits logistic mixed models and this is something that Stata does quite well. So I regularly get mailings about updates and I am always just blown away at the expense involved in maintaining the most current version of this software, particularly when you used the intercooled version.  It's relatively frequently updated (a good thing) but these updates are expensive (a bad thing for people without generous institutional subsidies). So, let me just start by saying that free is good.

This actually brings up a bit of a pet peeve of mine regarding training in US population centers.  We have these generous programs to train population scientists and policy-makers from the poor countries of the world.  We bring them into our American universities and train them in demographic and statistical methods on machines run by proprietary (and expensive!) operating systems and using extremely expensive proprietary software.  These future leaders will graduate and go back home to Africa, Asia, eastern Europe, or Latin America. There, they probably won't have access to computers with the latest hardware running the most recent software.  Most of their institutions can't afford expensive site licenses to the software that was on every lab machine back at Princeton or UCLA or Michigan or [fill in your school's name here]. This makes it all the more challenging to do the work that they were trained to do and leaves them just that much more behind scholars in advanced industrial nations.  If our population centers had labs with computers running Linux, taught statistics and numerical methods using R, and had students write LaTeX papers, lecture slides, and meeting posters using, say, Emacs rather than some bloated word-processor whose menu structure seems to change every release, then I think we would be doing a real service to the future population leaders of the developing world. But let's return to the question at hand, other than the fact that it's free -- which isn't such an issue for someone with a funded lab at an American University -- why should anyone take the trouble to learn R? I can think of seven reasons off the top of my head.

(1) R is what is used by the majority of academic statisticians.  This is where new developments are going to be implemented and, perhaps more importantly, when you seek help from a statistician or collaborate with one, you are in a much better position to benefit from the interaction if you share a common language.

(2) R is effectively platform independent.  If you live in an all-windows environment, this may not be such a big deal but for those of us who use Linux/Mac and work with people who use windows, it's a tremendous advantage.

(3) R has unrivaled help resources.  There is absolutely nothing like it.  First, the single best statistics book ever is written for R (Venables & Ripley, Modern Applied Statistics in S -- remember R is a dialect of S).  Second, there are all the many online help resources both from r-project.org and from many specific lists and interest groups. Third, there are proliferating publications of excellent quality. For example, there is the new Use R series. The quantity and quality of help resources is not even close to matched by any other statistics application.  Part of the nature of R -- community constructed, free software -- means that the developers and power users are going to be more willing to provide help through lists, etc. than someone in a commercial software company. The quality and quantity of help for R is particularly relevant when one is trying to teach oneself a new technique of statistical method.

(4) R makes the best graphics. Full stop. I use R, Matlab, and Mathematica.  The latter two applications have a well-deserved reputation for making great graphics, but I think that R is best.  I quite regularly will do a calculation in Matlab and export the results to R to make the figure.  The level of fine control, the intuitiveness of the command syntax (cf. Matlab!), and the general quality of drivers, etc. make R the hands-down best.  And let's face it, cool graphics sell papers to reviewers, editors, etc.

(5) The command-line interface -- perhaps counterintuitively -- is much, much better for teaching.  You can post your code exactly and students can reproduce your work exactly.  Learning then comes from tinkering. Now, both Stata and SAS allow for doing everything from the command line with scripts like do-files.  But how many people really do that?  And SPSS...

(6) R is more than a statistics application.  It is a full programming language. It is designed to seamlessly incorporate compiled code (like C or Fortran) which gives you all the benefits of a interactive language while allowing you to capitalize on the speed of compiled code.

(7) The online distribution system beats anything out there.

Oh, and let's face it, all the cool kids use it...

Human Ecology, Infectious Disease, Statistics

Uncertainty and Fat Tails

4 Comments

A major challenge in science writing is how to effectively communicate real, scientific uncertainty.  Sometimes we just don't know have enough information to make accurate predictions.  This is particularly problematic in the case of rare events in which the potential range of outcomes is highly variable. Two topics that are close to my heart come to mind immediately as examples of this problem: (1) understanding the consequences of global warming and (2) predicting the outcome of the emerging A(H1N1) "swine flu" influenza-A virus.

Harvard economist Martin Weitzman has written about the economics of catastrophic climate change (something I have discussed before).  When you want to calculate the expected cost or benefit of some fundamentally uncertain event, you basically take the probabilities of the different outcomes and multiply them by the utilities (or disutilities) and then sum them.  This gives you the expected value across your range of uncertainty.  Weitzman has noted that we have a profound amount of structural uncertainty (i.e., there is little we can do to become more certain on some of the central issues) regarding climate change.  He argues that this creates "fat-tailed" distributions of the climatic outcomes (i.e., the disutilities in question).  That is, the probability of extreme outcomes (read: end of the world as we know it) has a probability that, while it's low, isn't as low as might make us comfortable.

A very similar set of circumstances besets predicting the severity of the current outbreak of swine flu.  There is a distribution of possible outcomes.  Some have high probability; some have low.  Some are really bad; some less so.  When we plan public health and other logistical responses we need to be prepared for the extreme events that are still not impossibly unlikely.

So we have some range of outcomes (e.g., the number of degrees C that the planet warms in the next 100 years or the number of people who become infected with swine flu in the next year) and we have a measure of probability associated with each possible value in this range. Some outcomes are more likely and some are less.  Rare events are, by definition, unlikely but they are not impossible.  In fact, given enough time, most rare events are inevitable.  From a predictive standpoint, the problem with rare events is that they're, well, rare.  Since you don't see rare events very often, it's hard to say with any certainty how likely they actually are.  It is this uncertainty that fattens up the tails of our probability distributions.  Say there are two rare events.  One has a probability of 10^{-6} and the other has a probability of 10^{-9}. The latter is certainly much more rare than the former. You are nonetheless very, very unlikely to ever witness either event so how can you make any judgement that the one is a 1000 times more likely than the other?

Say we have a variable that is normally distributed.  This is the canonical and ubiquitous bell-shaped distribution that arises when many independent factors contribute to the outcome. It's not necessarily the best distribution to model the type of outcomes we are interested in but it has the tremendous advantage of familiarity. The normal distribution has two parameters: the mean (\mu) and the standard deviation (\sigma).  If we know \mu and \sigma exactly, then we know lots of things about the value of the next observation.  For instance, we know that the most likely value is actually \mu and we can be 95% certain that the value will fall between about -1.96 and 1.96. 

Of course, in real scientific applications we almost never know the parameters of a distribution with certainty.  What happens to our prediction when we are uncertain about the parameters? Given some set of data that we have collected (call it y) and from which we can estimate our two normal parameters \mu and \sigma, we want to predict the value of some as-yet observed data (which we call \tilde{y}).  We can predict the value of \tilde{y} using a device known as the posterior predictive distribution.  Essentially, we average our best estimates across all the uncertainty that we have in our data. We can write this as

p(\tilde{y}|y,\mu,\sigma) = \int \int p(y|\mu,\sigma) p(\mu,\sigma|y) d\mu d\sigma.

 

OK, what does that mean? p(y|\mu,\sigma) is the probability of the data, given the values of the two parameters.  This is known as the likelihood of the data. p(\mu,\sigma|y) is the probability of the two parameters given the observed data.  The two integrals mean that we are averaging the product p(y|\mu,\sigma)p(\mu,\sigma|y) across the range of uncertainty in our two parameters (in statistical parlance, "integrating" simply means averaging).  

If you've hummed your way through these last couple paragraphs, no worries.  What really matters are the consequences of this averaging.

When we do this for a normal distribution with unknown standard deviation, it turns out that we get a t-distribution.  t-distributions are characterized by "fat tails." This doesn't mean they look like this. What it means is that the probabilities of unlikely events aren't as unlikely as we might be comfortable with.  The probability in the tail(s) of the distribution approach zero more slowly than an exponential decay.  This means that there is non-zero probability on very extreme events. Here I plot a standard normal distribution in the solid line and a t-distribution with 2 (dashed) and 20 (dotted) degrees of freedom.

Standard normal (solid) and t distributions with 2 (dashed) and 20 (dotted) df.

We can see that the dashed and dotted curves have much higher probabilities at the extreme values.  Remember that 95% of the normal observations will be between -1.96 and 1.96, whereas the dashed line is still pretty high for outcome values beyond 4.  In fact, for the dashed curve,  95% of the values fall between -4.3 and 4.3. In all fairness, this is a pretty uncertain distribution, but you can see the same thing with the dotted line (where the 95% internal interval is plus/minus 2.09).  Unfortunately, when we are faced with the types of structural uncertainty we have in events of interest like the outcome of global climate change or an emerging epidemic, our predictive distributions are going to be more like the very fat-tailed distribution represented by the dashed line.

As scientists with an interest in policy, how do we communicate this type of uncertainty? It is a very difficult question.  The good news about the current outbreak of swine flu is that it seems to be fizzling in the northern hemisphere. Despite the rapid spread of the novel flu strain, sustained person-to-person transmission is not occurring in most parts of the northern hemisphere. This is not surprising since we are already past flu season.  However, as I wrote yesterday, it seems well within the realm of possibility that the southern hemisphere will be slammed by this flu during the austral winter and that it will come right back here in the north with the start of our own flu season next winter.  What I worry about is that all the hype followed by a modest outbreak in the short-term will cause people to become inured to public health warnings and predictions of potentially dire outcomes. I don't suppose that it will occur to people that the public health measures undertaken to control this current outbreak actually worked (fingers crossed).  I think this might be a slightly different issue in the communication of science but it is clearly tied up in this fundamental problem of how to communicate uncertainty.  Lots to think about, but maybe I should get back to actually analyzing the volumes of data we have gathered from our survey!

Statistics

Statistics and Election Forecasting

Leave a comment

With election day past us now, I have a moment to reflect upon how uncanny were Nate Silver and crew's predictions of the election.  I became quite a FiveThirtyEight.com junky as the election approached and I think that the stunning success that they demonstrated in predicting all sorts of elections yesterday holds lessons for the way we do social science more generally.

The predictions at  FiveThirtyEight.com start with the basic premise that all polls are wrong but when taken in aggregate, they provide a great deal of very useful information.  Basically, they aggregated information from a large number of polls and weighted the contributions of the different polls based on their reliability scores.  These reliability scores are based on three things: (1) the pollster's accuracy in predicting recent election outcomes, (2) the poll's sample size, and (3) the recentness of the poll.  Pollsters who have done well in the past, typically do well in the present.  Polls of many potential voters are more precise than polls of a small number of voters.  Recent polls are more salient that polls taken a while ago.  The site provides a very detailed account of how it calculates its reliability scores, particularly in terms of pollster accuracy.  The weighted polling data were then further adjusted for trends in polls. For their projections, they then took the adjusted polling data and ran regressions on a variety of social and demographic variables for the different polled populations. Using these regressions, they were able to calculate a snapshot in time of how each state would likely vote if the vote were held on that day.  These snapshots were then projected to the November election.  Finally, they ran simulations over their projections (10,000 at a time) to understand how the various forms of uncertainty were likely to affect the outcomes.

FiveThirtyEight.com projected that Obama would win with 348.6 electoral votes.  The current count is (provisionally) 364.  Pretty darn good, given the manifold uncertainties.  What is even more stunning is a comparison of the projected/realized election maps.  Here is the actual electoral map (as of today, 5 November at 21:00 PST):

Electoral Map on 6 November 2008

 

Here is their final proejction:

Final fivethirtyeight.com Projection

Hard to imagine it being much righter...

In the social sciences - especially in anthropology -- we gather crappy data all the time. There is generally much more that we can do with these data than is usually done.  I find that the fivethirtyeight.com methodology has a lot to offer social science.  In particular, I really like the focus on prediction of observable quantities. Too often, we get caught up in the cult of the p-value and focused on things that ultimately unknowable and unmeasurable (the "true" value of a test statistic, for example).  Predicting measurables and then adjusting the weight one gives particular predictions based on their past performance seems like a very reasonable tool for other types of social (and natural) science applications. 

I need to think more about specific anthropological applications, but I am intrigued at least by the idea that one could use the clearly biased results of some assay of behavior to nonetheless make accurate predictions of some outcome of interest. In the case of elections, the assay is polling.  In the anthropological case, it might be the report of an informant in one's ethnographic investigation.  We know that informants (like pollsters, or ethnographers for that matter) may have a particular agenda. But if we could compare the predictions based on an ethnographic interview with a measurable outcome, adjust the predictions based on predictive performance and then aggregate the predictions of many informants, we might have a powerful, scientific approach to some ethnographic questions that acknowledges the inherent bias and subjectivity of the subject matter but nonetheless makes meaningful scientific predictions. 

I'm just thinking out loud here.  Clearly, I need to add some more specifics to have this make sense. Perhaps I will take up this thread again in the future.  For now, I just want to pass along kudos once more to FiveThirtyEight.com for a job very well done.

Statistics

Truly Excellent Statistical Graphic

Leave a comment

The figure that appeared on MediaCurves.com (the link to which I found here) following the second presidential debate last night was a truly outstanding example of communicating complex information using simple, effective graphical presentation.

The figure shows the responses of 1004 respondents to the question of who won the debate.  The graphic summarizes quite a bit of information in a readily understandable manner.  What I find particularly striking is (1) 20% of self-reported Republicans think that Barack Obama won and (2) only 68% of self-reported Republicans think that John McCain won.

Not necessarily related to statistical graphics, it will be interesting to see if Nate Silver is as good at predicting presidential elections as he is at predicting baseball outcomes.