This week in class I tried to take on the topic of complexity, as in "complex systems theory." Complexity is a very important topic in human ecology, and biosocial science more generally. It's also a topic that worries me a bit. It worries for two reasons. First, it seems all too easy for people to fall in with the cult of complexity and I believe that the weight of evidence shows very clearly that people are not at their best when they are associated with cults. If a perspective on science provides novel (especially testable!) insights, then I'm all for it. When it takes on the doctrinaire elements of a religion, then I'm less convinced of its value. The second reason complexity worries me is clearly related to the first. I am continually frustrated by anthropologists who, when confronted with complexity, throw their hands up and say it's too complex to make predictions, why bother to do science or understand the principles underlying the system? You'd need to be trained as a theoretical physicist to understand the theory and people who think they understand something are just deluding themselves (or at least the rest of us) with a masculinist, hegemonic fantasy anyway. Let's just tell a narrative (preferably peppered with some mind-numbing post-structuralist social theory). Better, perhaps, that we describe history. I think that this view is misguided to say the least (though I agree that history is fundamentally important).
There are three very influential reviews, all written for the Annual Review of Anthropology (when Bill Durham was editor, might I add), by eminent ecological anthropologists that have fed this perspective. Ian Scoones, Steve Lansing, and William Baleé each wrote a review between 1999 and 2006 more or less on the topic of complexity in human ecology. Scoones (1999) reviewed the 'New Ecology' and its implications for the social science. Lansing (2003) introduced complexity proper , and Baleé (2006) wrote about 'Historical Ecology.' I think its probably fair to say that each of these authors has a different sensibility regarding the role of science in anthropology.
Baleé advocates for the perspective of historical ecology, which emphasizes historical contingency and human agency in shaping landscapes. He seems to conflate systems ecology with an equilibrium episteme, noting that historical ecology is 'at odds with systems ecology' (Baleé 2006: 81) for the latter approach's inability to allow human agency to increase biodiversity in some cases. This is an odd critique, since there is nothing inherent in any systems theory of ecological dynamics that makes this the case. He is also critical of island biogeography theory of MacArthur & Wilson (1967) because of its lack of attention to human agency as a cause of species invasions. Again, there is nothing inherent in island biogeography theory -- or its modern inheritor, metapopulation biology -- that excludes human agency as a mechanism for colonization. Presumably, the interested anthropologist could construct a model that included human facilitation of species invasions and explore both the transient and asymptotic (e.g., equilibrium) properties of this model.
Systems ecology, according to Baleé's review, may have provided mathematical rigor to human ecology but it was static, ahistorical, and neglected political processes, a point first noted by Wolf in his Europe and the People without History. While it is certainly true that cultural ecologists studied relatively unstratified cultures (typically in isolation of other parts of the (human) world economic system), once again, there is nothing intrinsic in cultural ecology that makes this necessary. The idea of a cultural core ("the constellation of features which are most closely related to subsistence activities and economic arrangements" (Steward 1955:37)), central to Steward's cultural ecology, is entirely applicable to stratified societies. It is more complex but that doesn't make it irrelevant. Similarly, it seems that Steward's multilinear evolutionary theory of culture, with its focus on broad cross-cultural patterns but emphasis of local particularities is also largely compatible with the tenets of historical ecology. I think that it is a fundamental misapprehension that every anthropologist who studies subsistence of face-to-face groups, following in the tradition of Julian Steward, is unaware of the larger political entanglements of foraging, farming, or pastoral people in a larger world political-economic system (see, e.g., Doug Bird's nice essay on the politics of Martu foraging). There is just a conditionality -- or 'bracketing' if you prefer the phenomenological term -- of subsistence activities. Given that the Martu or Hadza (or whoever) forage, how do they go about doing it? What are the consequences for landscapes in which they are embedded? These are legitimate, important, and interesting questions. So are questions about broader political economy. A little secret: They're not mutually exclusive.
Lansing writes about complex systems proper, and about the phenomenon of emergence in particular. Emergence occurs when order arises solely out of local interactions and in the absence of central control. I agree completely with Lansing that an investigation of emergence is an important endeavor in ecological anthropology and, indeed, anthropology more generally. My concern that emerges from Lansing's paper is simply the idea that we have no hope of understanding anything without really complex nonlinear models -- models that are so complex they can only be instantiated in agent-based simulations. While I am engaged in the ideas of complex systems, I am not quite ready to give up on many traditional forms of analysis that use linear models. As we will see below, the devil is in the details in complex systems models and I don't think it's good for science to deprive ourselves of important suites of tools because of a priori assumptions about the nature of the systems we study. This statement should not be interpreted to mean that I think this is what Lansing is doing. I do worry about anthropologists who read this review being scared away from formal ecological analysis because the nonlinearity sounds scary.
It is Scoones (1999) who makes the most extreme statements about the consequences of complexity for human ecology. Regarding the three unifying themes around which the new human ecology was coalescing, he writes (1999: 490), "Third is the appreciation of complexity and uncertainty in social-ecological systems and, with this, the recognition of that prediction, management, and control are unlikely, if not impossible." I think that this statement, while it may be an accurate description of some unifying themes in recent human ecology is simply incorrect and more than a bit nihilist. In all fairness, Scoones goes on to ask what the alternatives to the usual practice are (1999: 495):
So, what is the alternative to such a managerialist approach? A number of suggestions have been made. They generally converge around what has been termed "adaptive management" (Holling 1978, Walters 1976). This approach entails incremental responses to environmental issues, with close monitoring and iterative learning built into the process, such that thresholds and surprises can be responded to (Folke et al 1998).
This is a fair statement, which is rather at odds with the previous quote. If prediction and management are impossible, why is adaptive management a viable replacement? Does adaptive management not entail making predictions and, well, managing? Of course it does.
I have a series of critical questions that must be addressed before we accede to excessive complexity and stop trying to understand the process underlying human ecology.
- With nonlinearity (as with stochasticity), the devil is in the details. What is the shape of the response? Sometimes nonlinear models are remarkably linear over the relevant parameter space and time scope. Sometimes they're not. We don't know unless we ask.
- What is the strength of the response? With nonlinearity, the thing that matters for the difficulty in prediction, sensitivity to initial conditions, etc. is the strength of response. Sometimes this strength is not that high and linear models work amazingly well.
- How big are the possible perturbations? We might be able to make quite good predictions if perturbations are small. Of course, we shouldn't assume that perturbations are always small (as much classical analysis does). This is an empirical question.
- What is the effect of random noise? Some of the deterministic models with exotic dynamics collapse into pretty standard models in the presence of noise. Of course, sometimes randomness makes prediction even harder -- this is partly a function of the previous three points (i.e., the shape of nonlinearity, the strength of the response, and the size of perturbations).
A couple figures can illustrate two of these points. Consider the following hypothetical recruitment plot. On the x-axis, I have plotted the population size, while on the y-axis, I have plotted the number of recruits born. Suppose that the actual underlying process for recruitment was density-dependent (i.e., was nonlinear), as indicated by the dashed line. In this particular hypothetical case, you would not do all that badly with a linear model (solid line). As we move across three orders of magnitude, the difference in recruitment between the linear and nonlinear models is two births. The process of recruitment is nonlinear (i.e., it's density-dependent) but you would do just fine with predictions based on a linear model.
Taking up on Bob May's classic (1976) paper, we can use the logistic map (a discrete-time logistic population growth model) to look at strength of response. The logistic map is given by the following nonlinear difference equation  . We can plot the relationship between
. We can plot the relationship between 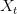 and
and 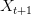 . This shows the classic symmetric, humped recruitment curve characteristic of the logistic model. Where a line
. This shows the classic symmetric, humped recruitment curve characteristic of the logistic model. Where a line 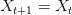 intersects the recruitment curve, the model has a fixed point. The stability of these fixed points is determined by the slope of the tangent line at the intersection of the curves. If the absolute value of this slope is greater than one, perturbations from the fixed point will grow -- the model is unstable. If the absolute value of this slope is less than one, then any trajectory in the neighborhood will return to the fixed point. The parameters used to make these figures create a complex 2-point series (i.e., the population oscillates between two fixed points) on the left-hand case, while for the right-hand case, there is a simple fixed point. By cranking up the parameter
intersects the recruitment curve, the model has a fixed point. The stability of these fixed points is determined by the slope of the tangent line at the intersection of the curves. If the absolute value of this slope is greater than one, perturbations from the fixed point will grow -- the model is unstable. If the absolute value of this slope is less than one, then any trajectory in the neighborhood will return to the fixed point. The parameters used to make these figures create a complex 2-point series (i.e., the population oscillates between two fixed points) on the left-hand case, while for the right-hand case, there is a simple fixed point. By cranking up the parameter  in the logistic map, we can induce more and more exotic dynamics. However, the key point here is that if the response is weak enough, the dynamics are not especially exotic at all. Note that we start to get the interesting behavior at values of
in the logistic map, we can induce more and more exotic dynamics. However, the key point here is that if the response is weak enough, the dynamics are not especially exotic at all. Note that we start to get the interesting behavior at values of 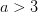 , or a tripling of population size each time step. Human populations do not grow nearly this fast. Not even close. This isn't to say that some human processes with nonlinear dynamics don't have very strong responses, but clearly not all must. Population growth is a pretty important problem for human ecology, and it's dynamics are unlikely to be really exotic. Maybe we can use some simple models to understand human population dynamics? See last week's post on the work of Tuljapurkar and colleagues for some exemplary contemporary work.
, or a tripling of population size each time step. Human populations do not grow nearly this fast. Not even close. This isn't to say that some human processes with nonlinear dynamics don't have very strong responses, but clearly not all must. Population growth is a pretty important problem for human ecology, and it's dynamics are unlikely to be really exotic. Maybe we can use some simple models to understand human population dynamics? See last week's post on the work of Tuljapurkar and colleagues for some exemplary contemporary work.
So, there are two cases where understanding the nature of the nonlinearity makes an enormous difference in how we make predictions and otherwise understand the system. Sometimes nonlinear models are effectively linear over important ranges of parameter space. Sometimes the response of a nonlinear model is small enough that the system shows very predictable, well-mannered dynamics. But just so you don't think that I don't think complexity is an issue, let's look at one more example. This model is from a classic study by Hastings and Powell (1991) showing chaos in a simple model of a food chain.
The model has three species: producer, primary consumer, secondary consumer; and it is a simple chain (secondary consumer eats primary consumer eats producer). Hastings and Powell chose the model parameters to be biologically realistic -- there's nothing inherently wacky about the way the model is set up. Using the same parameters that they use to produce their figure 2, I numerically solved their equations (using deSolve in R). The first plot shows the dynamics in time, with the bizarre oscillations in all three species.
In the second figure, I reproduce (more or less) their three-dimensional phase plot, which takes time out of the plot and instead plots the three population series directly against each other.
Finally, I plot some pair-wise phase-plots, which are easier to visualize than the false 3D image above.
On the whole, we see very complex behavior in a rather simple food chain. Hastings and Powell (1991: 901-902) summarize their findings: (1) contrary to conventional wisdom, they suggest that chaos need not be rare in nature, (2) chaotic behavior "need not lead to an erratic and unpatterned trajectory in time that one might infer from the usual (not mathematical) connotation of the word 'chaos'" and (3) time scales matter tremendously -- over short time scales, the behavior of the system is quite regular.
For me, the greatest lesson from the complex systems approach is the need to understand the specific details. Contrary to the inclination to throw up one's hands at the thought of a science of human ecology (let alone putting this science into practice with sensible management policies), it seems that the issues raised here mean that we should study these systems more, attempting to understand both their historical trajectories and the principles upon which they are organized. By all means, let's jettison old-fashioned ideas about typology and homeostasis in nature. No need to keep around the clockworks metaphor of ecological succession or the idea that the Dobe !Kung are Pleistocene remnants. Ecosystems, landscapes, whatever term you want to use, don't necessarily tend toward equilibria. Uncertainty is ubiquitous. People are part of these systems and have been for a long time. Good, we're agreed. But can we please not give up on using all the scientific tools we have at our disposal to understand these complex systems in which human beings are embedded? Anthropologists have much to contribute to this area, not the least of which is long-term, place-based research on human-environmental systems.
The lesson of prediction over the short-term is another issue that comes up repeatedly in the complex systems literature. I think that the work of George Sugihara and colleagues is especially good on this front. I have blogged (here and here) about a paper on which he is a co-author before (I should note that in this paper they suggest ways to make predictions of catastrophic events in complex systems with noise -- just sayin'). There is a nice, readable article in Scientific American on his work on fisheries that summarizes the issues. This work combines so many things that I like (demography, fish, statistics, theoretical ecology, California), it's a bit scary. Another nice, readable piece that also describes some of Sugihara's work in finance can be found in SEED magazine here.
This post is already too long. I clearly will need to write about the other topic for the week, risk and uncertainty, at a later date.
References
Baleé, W. 2006. The research program of historical ecology. Annual Review of Anthropology. 35:75-98.
Hastings, A., and T. Powell. 1991. Chaos in a three-species food chain. Ecology. 72 (3):896-903.
Lansing, J. S. 2003. Complex adaptive systems. Annual Review of Anthropology. 32:183-204.
MacArthur, R. H., and E. O. Wilson. 1967. The theory of island biogeography. Princeton: Princeton University Press.
May, R. M. 1976. Simple Mathematical-Models with Very Complicated Dynamics. Nature. 261 (5560):459-467.
Scoones, I. 1999. New Ecology and the social sciences: What prospects for a fruitful engagemnt? Annual Review of Anthropology. 28:479-507.





2 thoughts on “Complexity and Nihilism”