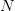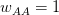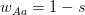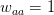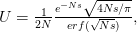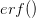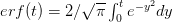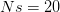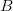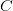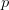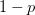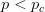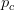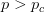I guess it's that time of the year. You know, when I recap, in my bittersweet way, the annual meeting of the American Anthropological Association? I am an anthropologist, yes, but I am deeply torn in my feelings for my discipline, my department, and my flagship (?) professional organization. The question mark arises because I am also a physical anthropologist and a demographer, so an argument can be made that my flagship professional organization is actually AAPA or PAA, but there is something about the unmarked category that is AAA. It's supposed to represent anthropologists, broadly construed. I honestly don't think that it does a very good job at this, but the reasons behind that are complex and I've only allocated myself a bit of time to blog since I'm desperately trying to catch up from all the travel I've done recently.
The meeting this year was in Chicago, which is a pretty amazing town. I stayed in the the Blackstone Renaissance Hotel, which was recently renovated in a lovely Art Deco theme. We did Chicago stuff. Tube steaks were eaten, the quantity of cheese that can be crammed into a deep-dish pizza was marveled at, beer was drunk.
AAA is a pretty bizarre scene. For starters, it's at the weirdest time. It seems like the peculiar timing of AAA during November must be disruptive for just about every academic anthropology department, particularly because it is nearly a week-long endeavor. It seems that the life in an American university carries on just fine without the anthropologists around for a week in the middle of the Fall term, thank you very much. A couple innovations this year struck me as particularly incongruous, given the content of much current scholarship in anthropology. First, anyone who registered for the meeting as a non-member was given a yellow badge holder to mark them as outsiders. This seemed a bit gratuitous. I'm not sure what's gained from such marking -- they already pay a substantially higher rate for the privilege of attending, do they also need to be shamed for their lack of faith? Second, in the hall outside the main bunch of conference rooms, there was a television that played a loop of anthropologists talking about how important anthropology is. This struck me as unnecessarily propagandistic and it's not at all clear to me who the target audience for this performance was. Presumably, those of us who were there already think that anthropology is a worthwhile endeavor. Seems to me that it's the rest of the world we need to convince. Once again, there appears to be almost nothing considered newsworthy to emerge from this meeting of 6,000+ scholars with the exception of a paper on the similarities in street-scanning behaviors by police and fashion scouts.
Another strange feature of AAAs is that computers, cables, remotes, laser-pointers, etc. were not provided in the conference rooms but needed to be provided by the session chairs. This is the first time I've experienced this in years at a major conference and it definitely slowed us down quite a bit at the start of our session. I'm not sure what was going on with that. Maybe the budget to pay for AV services was already spent on the fancy video production that reminded us how important we all are?
This year, I organized and chaired a session, which was sponsored by EAS, on social network analysis in evolutionary anthropology. Unfortunately for the EAS party-goers from the previous night, the session ran at 08:00 on Saturday morning. Despite this challenge, the room was packed and the audience generally seemed into it. We had great talks by Stanford's own Elly Power and Ashley Hazel. Elly talked about her amazing dissertation research on using social capital to understand costly displays of religious devotion in southern India. Ashley talked about her dissertation work in the School of Natural Resources and the Environment on mobility and the changing landscape of STI risk in Kaokoland, northern Namibia. David Nolin, one of our discipline's most talented young methodologists, presented a very clever test of generalized reciprocity using dichotomous exchange data from his work in Lamalera in Indonesia. Ben Hannowell, yet another talented methodologist to come out of the WSU/UW IGERT program, discussed his collaborative work with Zack Almquist on inferring dominance structure from tournament graphs. The always marvelous Rebecca Sear talked about her recent synthetic work on the effects of kin on fertility (kinship, of course, is the classic application of networks in anthropology since genealogies are just special cases of graphs). John Ziker presented a network-based approach to understanding food sharing and reciprocity from his terrific ethnographic work in Siberia. I closed out the talks with my own combination history of anthropological (and ethological) contributions to social network analysis and pep talk to encourage anthropologists to be confident about their methods and have the courage to innovate new ones the way people like John Barnes or Clyde Mitchell or Elizabeth Bott or Kim Romney or Russ Bernard did!
After schmoozing for a bit post-session, I headed over to the Saturday EAS session on methodological advances in experimental games. While I didn't see all the talks, the ones I saw were pretty cool. In general, I have mixed feelings about experimental economic games. There are lots of results and some fairly convincing stories to go along with some of the results. However, absent of context, I really wonder what they are measuring and, if they are indeed measuring something, whether it is actually interesting. This session made some real progress in dealing with this question and I think it really highlighted the comparative advantage of anthropologists in the multi-disciplinary landscape of twenty-first century behavioral science. While economists such as Loewenstein (1999) might lament the fact that there is no way to play context-less games and that this jeopardizes the validity and generality of such experimental games, anthropologists are experts in thinking specifically about context and its effect on behavior. Furthermore, anthropologists are still the go-to researchers for providing contextual diversity. In this session, we heard about experimental games played in Bolivia, Siberia, Fiji, and on the streets of Las Vegas. One talk in this session that particularly impressed me was given by Drew Gerkey, who is currently a post-doc at SESYNC in Annapolis, Maryland (and soon to be an assistant professor at Oregon State University -- Go Beavs!). I was at SESYNC earlier in the week and got a chance to talk pretty extensively with him about this work. Drew makes the point that seems obvious now that I've heard (a sign of an important idea) that, in the evolution of cooperation literature, the counterfactual scenario to cooperation is frequently untenable. One does not simply go it alone when one is a hunter/fisher in Siberia. Drew also designed a number of very clever experimental games that fit the types of social dilemmas faced by his Siberian interlocutors. Very nice work indeed.
In addition to the sessions I attended, it was nice to see and chat with various smart, fun people I know who sometimes find their way to AAAs. I missed my partner in crime from last year's AAA, Charles Roseman, who left the day I arrived, probably too bloated from the binge on Chicago's amazing food he no doubt shared with Fernando Armstron-Fumero to be of much use to anyone. However, I got to see Siobhan Mattison, Brooke Scelza, Brian Wood, Rick Bribiescas, Mary Shenk, Aaron Blackwell, Pete Kirby and, briefly, Shauna Burnsilver and Dan Hruschka. Despite my general misgivings about the conference, it is nice to have an excuse to see so many cool people in one place at one time.