A new paper written by Dan Salkeld (formerly of Stanford), Kerry Padgett (CA Department of Public Health), and myself just came out in the journal Ecology Letters this week.
One of the most important ideas in disease ecology is a hypothesis known as the "dilution effect". The basic idea behind the dilution effect hypothesis is that biodiversity -- typically measured by species richness, or the number of different species present in a particular spatially defined locality -- is protective against infection with zoonotic pathogens (i.e., pathogens transmitted to humans through animal reservoirs). The hypothesis emerged from analysis of Lyme disease ecology in the American Northeast by Richard Ostfeld and his colleagues and students from the Cary Institute for Ecosystem Studies in Millbrook, New York. Lyme disease ecology is incredibly complicated, and there are a couple different ways that the dilution effect can come into play even in this one disease system, but I will try to render it down to something easily digestible.
Lyme disease is caused by a spirochete bacterium Borrelia burgdorferi. It is a vector-borne disease transmitted by hard-bodied ticks of the genus >Ixodes. These ticks are what is known as hemimetabolous, meaning that they experience incomplete metamorphosis involving larval and nymphal stages. Rather than a pupa, these larvae and nymphs resemble little bitty adults. An Ixodes tick takes three blood meals in its lifetime: one as a larva, once as a nymph, once as an adult. At different life-cycle stages, the ticks have different preferences for hosts. Larval ticks generally favor the white-footed mouse (Peromyscus leucopus) for their blood meal and this is where the catch is. It turns out that white-footed mice are extremely efficient reservoirs for Lyme disease. In fact, an infected mouse has as much as a 90% chance of transmitting infection to a larva feeding on it. The larvae then molt into nymphs and overwinter on the forest floor. Then, in spring or early summer a year after they first hatch from eggs, nymphs seek vertebrate hosts. If an individual tick acquired infection as a larva, it can now transmit to its next host. Nymphs are less particular about their choice of host and are happy to feed on humans (or just about any other available vertebrate host).
This is where the dilution effect comes in. The basic idea is that if there are more potential hosts such as chipmunks, shrews, squirrels, or skunks, there are more chances that an infected nymph will take a blood meal on a person. Furthermore, most of these hosts are much less efficient at transmitting the Lyme spirochete than are white-footed mice. This lowers the prevalence of infection and makes it more likely that it will go extinct locally. It's not difficult to imagine the dilution effect working at the larval stage blood-meal too: if there are more species present (and the larvae are not picky about their blood meal), the risk of initial infection is also diluted.
In the highly-fragmented landscape of northeastern temperate woodlands, when there is only one species in a forest fragment, it is quite likely that it will be a white-footed mouse. These mice are very adaptable generalists that occur in a wide range of habitats from pristine woodland to degraded forest. Therefore, species-poor habitats tend to have mice but no other species. The idea behind the dilution effect is that by adding different species to the baseline of a highly depauperate assemblage of simply white-footed mice, the prevalence of nymphal infection will decline and the risk for zoonotic infection of people will be reduced.
It is not an exaggeration to say that the dilution-effect hypothesis is one of the two or three most important ideas in disease ecology and much of the explosion of interest in disease ecology can be attributed in part to such ideas. The dilution effect is also a nice idea. Wouldn't it be great if every dollar we invested in the conservation of biodiversity potentially paid a dividend in reduced disease risk? However, its importance to the field or the beauty of the idea do not guarantee that it is actually scientifically correct.
One major issue with the dilution effect hypothesis is its problem with scale, arguably the central question in ecology. Numerous studies have shown that pathogen diversity is positively related to overall biodiversity at larger spatial scales. For example, in an analysis of global risk of emerging infectious diseases, Kate Jones and her colleagues form the London Zoological Society showed that globally, mammalian biodiversity is positively associated with the odds of an emerging disease. Work by Pete Hudson and colleagues at the Center for Infectious Disease Dynamics at Penn State showed that healthy ecosystems may actually be richer in parasite diversity than degraded ones. Given these quite robust findings, how is it that diversity at a smaller scale is protective?
We use a family of statistical tools known as "meta-analysis" to aggregate the results of a number of previous studies into a single synthetic test of the dilution-effect hypothesis. It is well known that inferences drawn from small samples generally have lower precision (i.e., the estimates carry more uncertainty) than inferences drawn from larger samples. A nice demonstration of this comes from the classical asymptotic statistics. The expected value of a sample mean is the "true mean" of a normal distribution and the standard deviation of this distribution is given by the standard error, which is defined as the standard deviation of the distribution divided by the square root of the sample size. Say that for two studies we estimate the standard deviation of our estimate of the mean to be 10. In the first study, this estimate is based on a single observation, whereas in the second, it is based on a sample of 100 observations. The estimated of the mean in the second study is 10 times more precise than the estimate based on the first because 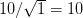 while
while 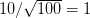 .
.
Meta-analysis allows us to pool estimates from a number of different studies to increase our sample size and, therefore, our precision. One of the primary goals of meta-analysis is to estimate the overall effect size and its corresponding uncertainty. The simplest way to think of effect size in our case is the difference in disease risk (e.g., as measured in the prevalence of infected hosts) between a species rich area and a species poor area. Unfortunately, a surprising number of studies don't publish this seemingly basic result. For such studies, we have to calculate a surrogate of effect size based on the reported test statistics of the hypothesis that the authors report. This is not completely ideal -- we would much rather calculate effect sizes directly, but to paraphrase a dubious source, you do a meta-analysis with the statistics that have been published, not with the statistics you wish had been published. On this note, one of our key recommendations is that disease ecologists do a better job reporting effect sizes to facilitate future meta-anlayses.
In addition to allowing us to estimate the mean effect size across studies and its associated uncertainty, another goal of meta-analysis is to test for the existence of publication bias. Stanford's own John Ioannidis has written on the ubiquity of publication bias in medical research. The term "bias" has a general meaning that is not quite the same as the technical meaning. By "publication bias", there is generally no implication of nefarious motives on the part of the authors. Rather, it typically arises through a process of selection at both the individual authors' level and the institutional level of the journals to which authors submit their papers. An author, who is under pressure to be productive by her home institution and funding agencies, is not going to waste her time submitting a paper that she thinks has a low chance of being accepted. This means that there is a filter at the level of the author against publishing negative results. This is known as the "file-drawer effect", referring to the hypothetical 19 studies with negative results that never make it out of the authors' desk for every one paper publishing positive results. Of course, journals, editors, and reviewers prefer papers with results to those without as well. These very sensible responses to incentives in scientific publication unfortunately aggregate into systematic biases at the level of the broader literature in a field.
We use a couple methods for detecting publication bias. The first is a graphical device known as a funnel plot. We expect studies done on large samples to have estimates of the effect size that are close to the overall mean effect because estimates based on large samples have higher precision. On the other hand, smaller studies will have effect-size estimates that are more distributed because random error can have a bigger influence in small samples. If we plot the precision (e.g., measured by the standard error) against the effect size, we would expect to see an inverted triangle shape -- or a funnel -- to the scatter plot. Note -- and this is important -- that we expect the scatter around the mean effect size to be symmetrical. Random variation that causes effect-size estimates to deviate from the mean are just as likely to push the estimates above and below the mean. However, if there is a tendency to not publish studies that fail to support the hypothesis, we should see an asymmetry to our funnel. In particular, there should be a deficit of studies that have low power and effect-size estimates that are opposite of the hypothesis. This is exactly what we found. Only studies supporting the dilution-effect hypothesis are published when they have very small samples. Here is what our funnel plot looked like.
Note that there are no points in the lower right quadrant of the plot (where species richness and disease risk would be positively related).
While the graphical approach is great and provides an intuitive feel for what is happening, it is nice to have a more formal way of evaluating the effect of publication bias on our estimates of effect size. Note that if there is publication bias, we will over-estimate our precision because the studies that are missing are far away from the mean (and on the wrong side of it). The method we use to measure the impact of publication bias on our estimate of uncertainty formalizes this idea. Known as "trim-and-fill", it uses an algorithm to find the most divergent asymmetric observations. These are removed and the precision of the mean effect size is calculated. This sub-sample is known as the "truncated" sample. Then a sample of missing values is imputed (i.e., simulated from the implied distribution) and added to the base sample. This is known as the "augmented" sample. The precision is then re-calculated. If there is no publication bias, these estimates should not be too different. In our sample, we find that estimates of precision differ quite a bit between the truncated and augmented samples. We estimate that between 4-7 studies are missing from the sample.
Most importantly, we find that the 95% confidence interval for our estimated mean effect size crosses zero. That is, while the mean effect size is slightly negative (suggesting that biodiversity is protective against disease risk), we can't confidently say that it is actually different than zero. Essentially, our large sample suggests that there is no simple relationship between disease risk and biodiversity.
On Ecological Mechanisms One of the main conclusions of our paper is that we need to move beyond simple correlations between species richness and disease risk and focus instead on ecological mechanisms. I have no doubt that there are specific cases where the negative correlation between species richness and disease risk is real (note our title says that we think this link is idiosyncratic). However, I suspect where we see a significant negative correlation, what is really happening is that some specific ecological mechanism is being aliased by species richness. For example, a forest fragment with a more intact fauna is probably more likely to contain predators and these predators may be keeping the population of efficient reservoir species in check.
I don't think that this is an especially controversial idea. In fact, some of the biggest advocates for the dilution effect hypothesis have done some seminal work advancing our understanding of the ecological mechanisms underlying biodiversity-disease risk relationships. Ostfeld and Holt (2004) note the importance of predators of rodents for regulating disease. They also make the very important point that not all predators are created equally when it comes to the suppression of disease. A hallmark of simple models of predation is the cycling of abundances of predators and prey. A specialist predator which induces boom-bust cycles in a disease reservoir probably is not optimal for infection control. Indeed, it may exacerbate disease risk if, for example, rodents become more aggressive and are more frequently infected in agonistic encounters with conspecifics during steep growth phases of their population cycle. This phenomenon has been cited in the risk of zoonotic transmission of Sin Nombre Virus in the American Southwest.
I have a lot more to write on this, so, in the interest of time, I will end this post now but with the expectation that I will write more in the near future!