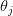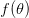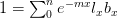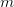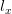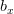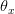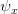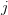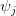Tag Archives: life history theory

Evolution

Genetic Architecture of Maize Flowering Time

2 Comments

There is a really cool paper by Buckler and colleagues in the current issue of Science.  The basic gist of this paper is that flowering time in maize (Zea mays) is not controlled by any large-effect genes (actually quantitative trait loci or QTLs -- these are positions in the genome that are associated with genes underlying a particular trait).  Instead, flowering time is controlled by lots of different QTLs, all with small effect.  I know what you're saying: "this fool anthropologist has really gone off the deep end this time. Why would he ever care about such boring stuff?!" Ah, but this is anything but boring and it has a very clear relevance to the evolution of life histories, human included.

Genes are discrete entities.  Yet we know that they code for things that can essentially vary continuously like stature or age at first reproduction. Probably the simplest (and remarkably general, even though this isn't how we learn about genetics in high school) way to think of genes is on-off switches.  At a particular locus, if you have allele A you get a +1 on your phenotype.  If you have allele a you get a +0.  For a locus that has just these two alleles, the possible phenotypes (assuming no environmental inputs, gene-gene interactions, or anything exotic) are 0,1, and 2 corresponding to aa, Aa/aA, and AA genotypes respectively.  You get twice as many individuals with phenotype=1 because there are two ways of making the heterozygote but only one way of making each of the homozygotes.  This is more or less high school biology.

Now, let's say that our phenotype is controlled by not one locus but many.  If we can reasonably assume that the different loci are independent of each other (not a hard-and-fast assumption), then a famous result from probability theory has important bearing on the question at hand.  In particular, I'm referring to the normal approximation of the binomial distribution. The binomial distribution is the coin-flipping distribution: how many tails will you get if you toss a coin (with a probability of tails = 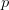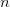p) n times.  It turns out that when the product 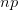np is greater than 5 (a very rough rule of thumb as there are other mild conditions) the binomial distribution -- a discrete probability distribution -- is very well approximated by a normal distribution -- a continuous one.  This is essentially how we get continuous phenotypes from discrete genotypes. The normal distribution is the limiting distribution whenever we have lots of small things drawn independently from the same process acting in an additive way (this is the mechanistic explanation of why the binomial can be approximated so well by the normal when 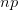np gets large).   Lots of loci, each acting in an additive way with small effect, leads to a normal distribution of a phenotype. When we have a few loci acting with large effect and possibly with strong interactions between loci (i.e., epistasis), the distribution of phenotypes is more likely to be more discrete (as with the one-locus, two-allele model).

Maize lives in a broad range of environments and, like us, it reproduces sexually. Unlike us, some plants can "self." That is, they don't need two to tango -- they reproduce sexually but a single individual provides both sets of gametes. The genetic architecture of flowering in two other genetically well-studied plants, rice and Arabidopsis (the ubiquitous mustard plant that is the favored model system of many developmental geneticists), does not show the same design as maize.  Both rice and Arabidopsis are selfing species.  It turns out that their genetic architecture resembles that of the simple additive system -- one with major gene effects and a more discrete distribution of flowering times. In these species, there is more evidence for gene-gene interactions and environmental inputs in the flowering time phenotype as well.

The fact that flowering time in maize is controlled by many loci with small additive effects means that the distribution of flowering time in any sizable population of maize will be approximately normally distributed.  There will be approximately continuous variation across the possible range of phenotypes and there will be far more individuals with phenotypes near the mean of the population.  In fact, about 95% of the phenotypes will be within ± 2 standard deviations of this mean.  Variation is the stuff of natural selection.  In order for evolution to occur by natural selection you need three things: (1) variation in the phenotype, (2) a heritable basis for this variation, and (3) differential fitness as a result of the variation.  No variation in the phenotype, no response to selection.  A trait with a nice continuous distribution -- as apparently maize flowering time is -- can respond with exquisite precision to selection imposed by the environment (assuming the population is big enough so that random events don't interfere). Maize shows an amazing degree of phenotypic diversity.  Flowering date is no exception with a range -- the landraces of maize vary in their developmental time between an astounding 2 and 11 months.

So there is plenty of phenotypic variation in maize to respond to selection.  Another important implication of the normal distribution of flowering time also means that local variation will fall into a fairly restricted range (that 95% of variation falling within ± 2 standard deviations thing).  If the distribution were more discrete, a field might contain two completely different flowering phenotypes.  In a species that requires out-crossing, producing gametes at two completely different times doesn't do you much good.  When you have a nice normal distribution of flowering times, there is variation, but it is not too extreme -- particularly in any local area.  This trait architecture allows maize to thread the evolutionary needle: enough variation to allow response to selection but not so much as to make reproduction impossible.

This type of architecture -- lots of small effects from independent genes -- is common in two other laboratory favorites, fruit flies and mice. It is also common in humans according to Flint & Mcckay (2009). Human stature, in particular, is a trait that has this kind of architecture. We know from the work of Rebecca Sear at the London School of Economics and her colleagues, that height predicts  reproductive success in humans (albeit in complex ways). Whether age at first reproduction (the human equivalent to flowering) is constructed the same way as maize flowering or human stature is an open question but I seriously doubt that we will find it to be controlled by a couple genes with large effect.  Such quantitative genetic architecture in complex life history traits bodes well for prediction.  We have a very well-developed theory that relates response to selection to the genetic variation in quantitative traits and the force of selection acting on those traits.  In order for this prediction to work well though, we need to also understand how life history traits are related to each other. That is, we need to not just know the means and standard deviations of one trait (like stature or age at sexual maturity).  We also need to know how traits are related to each other.  In other words, we need to measure the covariances between traits.  Fortunately, the normal approximation that we use for one trait can easily be extended to multiple traits, providing a nice framework for both estimation and prediction. I am working at this very moment on estimating the quantitative genetic relationships between human life history traits using a large genealogical database of a historical population.  More on this later...

Demography, Evolution

Gadgil & Bossert (1970)

1 Comment

I am currently teaching a class entitled "Demography and Life History Theory."  For this class, we read the classic paper by Madhav Gadgil and Bill Bossert, "Life Historical Consequences of Natural Selection." In preparing for class, I re-read this paper for about the twelfth time.  Something happened this time.  It really dawned on me what a spectacularly important paper this is.  Just about every important theme in life history theory is addressed in this paper and the analyses remain remarkably relevant.

One of the fundamental ideas this paper brought to life history theory is thinking about the convexity of the functions that describe both the fitness benefits and costs associated with the degree of reproductive effort.  In particular, Gadgil & Bossert show that iteroparity (i.e., repeated breeding) can only evolve if the function relating benefit to effort is concave or the function relating cost to effort is convex.  The figure shows a concave profit function and a linear cost.  Clearly, the maximal value of the difference between the profit and cost happens at some intermediate level of effort \theta_j.

Profit (solid line) and cost (dashed line) as a function of reproductive effort at at age j.

Maddeningly, Gadgil & Bossert invert the terms "convex" and "concave."  I'm sure there is a good historical explanation for this, but contemporary usage indicates that a continuous, twice differentiable function f(\theta) is convex if f''(\theta)>0.  That is a convex function shows increasing marginal returns to effort, whereas a concave function shows diminishing marginal returns to effort.

Their analysis focuses on a discrete-time form of Lotka's characterisitc equation:

1 = \sum_0^n e^{-mx} l_x b_x

where m is the Maulthusian parameter (the intrinsic rate of increase, r, in a density-independent population), l_x is the fraction surviving to age x, b_x is the birth rate (in daughters) to females age x.

What makes this approach so interesting and important is that the vital rates are functions of reproductive effort \theta_x at each age.  In addition to l_x and b_x being  functions of effort, they are also functions of "satisfaction" \psi_x, a measure of environmental quality.  Fertility at age x increases with effort and satisfaction.  Survivorship and growth decrease with effort and increase with satisfaction.  Fertility also increases with body size.

Gadgil and Bossert then maximize m subject to the biological constraints on intrinsic mortality, growth rate, and initial size, and the environmental constraints of satisfaction and mortality due to predation. They used an automatic computer to numerically solve their optimization problem.  They derive a number of quite general results for age-structured populations.

  1. Only when the profit function is concave or the cost function is convex can repeated breeding be optimal.
  2. Reproductive effort increases with age in repeated breeders.  George Williams arrived at a similar conclusion in 1966, but failed to consider the possibility that the fitness profit could decline with age.  Gadgil & Bossert arrive at this result with a much more general approach than that used by Williams.
  3. When mortality increases following some age j, reproductive effort increases for ages less than j.
  4. When reproductive potential increases slowly with size, reproductive effort will be lower at maturity, rise with age, and growth will continue beyond maturity.
  5. A uniform change in mortality -- affecting all ages equally -- will have no direct impact on reproductive effort.
  6. If the population is resource-limited, such a uniform change in mortality will increase satisfaction \psi_j with its consequent effects, including a lowering of age at first breeding and increase in reproductive effort.

I would have to say that this is the desert island paper for life history theory.  If you only ever read one paper (conditional on having the mathematics background to make it worthwhile), this is the one to read, even after 38 years.