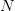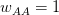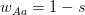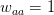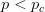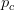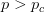Every once in a while someone asks me for advice on the platform to use for developing models of infectious disease. I typically make the same recommendations -- unless the person asking has something very specific in mind. This happened again today and I figured I would turn it into a blog post.
The answer depends largely on (1) what types of models you want to run, (2) how comfortable you are with programming, and (3) what local resources (or lack thereof) you might have to help you when you inevitably get stuck. If you are not comfortable with programming and you want to stick to fairly basic compartmental models, then something like Stella or Berkeley Madonna would work just fine. There are a few books that provide guidance on developing models in these systems. I have a book by Hannon and Ruth that is ten years old now but, if memory serves me correctly, was a pretty good introduction both to STELLA and to ecological modeling. They have a slightly newer book as well. Models created in both systems appear in the primary scientific literature, which is always a good sign for the (scientific) utility of a piece of software. These graphical systems lack a great deal of flexibility and I personally find them cumbersome to use, but they match the cognitive style of many people quite nicely, I think, and probably serve as an excellent introduction to mathematical modeling.
Moving on to more powerful, general-purpose numerical software...
Based on my unscientific convenience sample, I'd say that most mathematical epidemiologists use Maple. Maple is extremely powerful software for doing symbolic calculations. I've tried Maple a few times but for whatever reason, it never clicked for me. Because I am mostly self-taught, the big obstacle for me using Maple has always been the lack of resources either print or internet for doing ecological/epidemiological models in this system. Evolutionary anthropologist Alan Rogers does have some excellent notes for doing population biology in Maple.
Mathematica has lots of advantages but, for the beginner, I think these are heavily outweighed by the start-ups costs (in terms of learning curve). I use Mathematica some and even took one of their courses (which was excellent if a little pricey), but I do think that Mathematica handles dynamic models in a rather clunky way. Linear algebra is worse. I would like Mathematica more if the notebook interface didn't seem so much like Microsoft Word. Other platforms (see below) either allow Emacs key bindings or can even be run through Emacs (this is not a great selling point for everyone, I realize, but given the likely audience for Mathematica, I have always been surprised by the interface). The real power of Mathematica comes from symbolic computation and some of the very neat and eclectic programming tools that are part of the Mathematica system. I suspect I will use Mathematica more as time goes on.
Matlab, for those comfortable with a degree of procedural-style programming, is probably the easiest platform to use to get into modeling. Again, based on my unscientific convenience sample, my sense is that most quantitative population biologists and demographers use Matlab. There are some excellent resources. For infectious disease modeling in particular, Keeling and Rohani have a relatively new book that contains extensive Matlab code. In population biology, books by Caswell and Morris and Doak, both contain extensive Matlab code. Matlab's routines for linear algebra and solving systems of differential equations are highly optimized so code is typically pretty fast and these calculations are relatively simple to perform. There is a option in the preferences that allows you to set Emacs key bindings. In fact, there is code that allows you to run Matlab from Emacs as a minor mode. Matlab is notably bad at dealing with actual data. For instance, you can't mix and match data types in a data frame (spreadsheet-like structure) very easily and forget about labeling columns of a data frame or rows and columns of a matrix. While its matrix capabilities are unrivaled, there is surprisingly little development of network models, a real growth area in infectious disease modeling. It would be really nice to have some capabilities in Matlab to import and export various network formats, thereby leveraging Matlab's terrific implementation of sparse matrix methods.
Perhaps not surprisingly, the best general tool, I think, is R. This is where the best network tools can be found (outside of pure Java). R packages for dealing with social networks include the statnet suite (sna, network, ergm), igraph, graph, blockmodeling, RGBL, etc. (the list goes on). It handles compartmental models in a manner similar to Matlab using the deSolve package, though I think Matlab is generally a little easier for this. One of the great things about R is that it makes it very easy to incorporate C or Fortran code. Keeling and Rohani's book also contains C++ and Fortran code for running their models (and such code is generally often available). R and Matlab are about equally easy/difficult (depending on how you see it) to learn. Matlab is somewhat better with numerically solving systems of differential equations and R is much better at dealing with data and modeling networks. R can be run through Emacs using ESS (Emacs Speaks Statistics). This gives you all the text-editing benefits of a state-of-the-art text editor plus an effectively unlimited buffer size. It can be very frustrating indeed to lose your early commands in a Matlab session only to realize that you forgot to turn on the diary function. No such worries when your run R through Emacs using ESS.
One of the greatest benefits of R is its massive online (and, increasingly, print publishing) help community. I think that this is how R really trumps all the other platforms to be the obvious choice for the autodidacts out there.
I moved from doing nearly all my work in Matlab to doing most work in R, with some in Mathematica and a little still in Matlab. These are all amazingly powerful tools. Ultimately, it's really a matter of taste and the availability of help resources that push people to use one particular tool as much as anything else. This whole discussion has been predicated on the notion that one wants to use numerical software. There are, of course, compelling reasons to use totally general programming tools like C, Java, or Python, but this route is definitely not for everyone, even among those who are interested in developing mathematical models.