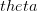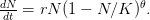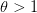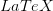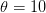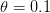In my last post, I wrote about a new paper by Myrskylä and colleagues in this past week's issue of Nature. Craig Hadley sent me a link to a criticism of this paper, and really more the science reporting of it in the Economist, written by Edward Hugh on the blog A Fist Full of Eruos within a couple hours of my writing. Hugh levels three criticisms against the Myrskylä et al. (2009) paper:
- The authors use total fertility rate (TFR) as their measure of fertility, even though TFR has known defects.
- The reference year (2005) was a peculiar year and so results based on comparisons of other years to it are suspect.
- Even if fertility increases below its nadir in highly developed countries, median age of the population could increase.
The first two of these are criticisms of the Myrskylä et al. (2009) Nature paper and it is these that I will address here. The third is really a criticism of the Economist's coverage of the paper.
TFR is a measure of fertility and in demographic studies like these, what we care about is people's fertility behavior. In a seminal (1998) paper, John Bongaarts and Griffith Feeney pointed out that as a measure of fertility TFR actually confounds two distinct phenomena: (1) the quantum of reproduction (i.e., how many babies) and (2) the tempo of reproduction (i.e., when women have them). Say we have two populations: A and B. In both populations, women have the same number of children on average. However, in population B, women delay their reproduction until later ages perhaps by getting married at older ages. In both populations, women have the same number of offspring but we would find that population A had the higher TFR. How is that possible? It is a result of the classic period-cohort problem in demography. As social scientists, demographers care about what actual people actually do. The problem is that measuring what actual people actually do over their entire lifetimes introduces some onerous data burdens and when you actually manage to get data for individual lifetimes, it is typically horribly out-of-date. For example, if you want to look at completed fertility, you need to look at women who are 50 years old or older at the time. This means that most of their childbearing happened between 20 and 30 years ago. Not necessarily that informative about current trends in fertility.
To overcome this problem, demographers frequently employ period measures of fertility, mortality, marriage, migration, etc. A period measure is essentially a cross-sectional measure of the population taken at a particular point in time. Rather than measuring the fertility of women throughout their lifetimes (i.e., looking at the fertility of a cohort of women where they are age 20, 30, 40, etc.), we measure the fertility of 20 year-olds, 30 year-olds, 40 year-olds, and so on at one particular point in time. We then deploy one of those demographers' fictions. We say that our cross-section of ages is a reflection of how people act over their life course. TFR is a period measure. We take the fertility rates measured for women ages 15-50 at a particular point in time (say, 2005) and sum them to yield the number of children ever born to a woman surviving to the end of her reproductive span if she reproduced at the average rate of the aggregate population.
Here is a simple (highly artificial) example of how this works. (Demographic purists will have to forgive me for reversing the axes of a Lexis diagram, as I think that having period along the rows of the table is more intuitive to the average person for this example.) The cells contain annual age specific fertility rates for each period. We calculate the period TFR by multiplying these values by the number of years in the age-class (which I assume is 5 for classes 10 and 40 and 10 for the others). In 1940, we see the beginning of trend in delayed fertility -- no women 15-20 (i.e., the "10 year-old" age class) have children. This foregone early fertility is made up for by greater fertility of 20-30 year-olds in 1940. Eventually, overall fertility declines -- at least in the periods for which we have full observations since the 1950, 1960, and 1970 cohorts have not completed their childbearing when the observations stop.

When we measure the TFR in 1930, we see that it is higher than the TFR in 1940 (3 vs. 2.5). Nonetheless, when we follow the two cohorts through to the end of their childbearing years (in blue for 1930 and red for 1940), we see that they eventually have the same cohort TFRs. That is, women in both cohorts have the same total number of children on average; it's just that the women in 1940 begin childbearing later. The behavior change is in tempo and not quantum and the period measure of fertility -- which is ostensibly a quantum measure since it is the total number of children born to a woman who survives to the end of her childbearing years -- is consequently distorted.
Bongaarts and Feeney (1998) introduced a correction to TFR that uses measures of birth order to remove the distortions. Myrskylä et al. (2009) were able to apply the Bongaarts/Feeney correction to a sub-sample (41) of their 2005 data. Of these 41 countries, they were able to calculate the tempo-adjusted TFR for 28 of the 37 countries with an HDI of 0.85 or greater in 2005. The countries with adjusted TFRs are plotted in black in their online supplement figure S2, reproduced here with permission.
 As one can easily see, the general trend of increasing TFR with HDI remains when the corrected TFRs are used. This graphical result is confirmed by a formal statistical test: Following the coincident TFR minimum/HDI in the 0.86-0.9 window, the slope of the best-fit line through the scatter is positive.
As one can easily see, the general trend of increasing TFR with HDI remains when the corrected TFRs are used. This graphical result is confirmed by a formal statistical test: Following the coincident TFR minimum/HDI in the 0.86-0.9 window, the slope of the best-fit line through the scatter is positive.
Hugh notes repeatedly that Myrskylä et al. (2009) anticipated various criticisms that he levels. For example, he writes "And you don’t have to rely on me for the suggestion that the Tfr is hardly the most desireable [sic] measure for what they want to do, since the authors themselves point this very fact out in the supplementary information." This seems like good honest social science research to me. I'm not entirely comfortable with the following paraphrasing, but here it goes. We do science with the data we have, not the data we wish we had. TFR is a widely available measure of fertility that allowed the authors to look at the relationship between fertility and human development over a large range of the HDI. Now, of course, having written a paper with the data that are available, we should endeavor to collect the data that we would ideally want. The problem with demographic research though is that we are typically at the whim of the government and non-government (like the UN) organizations that collect official statistics. It's not like we can go out and perform a controlled experiment with fixed treatments of human development and observe the resulting fertility patterns. So this paper seems like a good-faith attempt to uncover a pattern between human development and fertility. When Hugh writes "the only thing which surprises me is that nobody else who has reviewed the research seems to have twigged the implications of this" (i.e., the use of TFR as a measure of fertility), I think he is being rather unfair. I don't know who reviewed this paper, but I'm certain that they had both a draft of the paper that eventually appeared in the print edition of Nature and the online Supplemental material in which Myrskylä and colleagues discuss the potential weaknesses of their measures and evaluate the robustness of their conclusions. That's what happens when you submit a paper and it undergoes peer review. The pages of Nature are highly over-subscribed (as Nature is happy to tell you whenever it sends you a rejection letter). Space is at a premium and the type of careful sensitivity analysis that would be de rigeur in the main text of a specialist journal such as Demography, Population Studies, or Demographic Research, end up in the online supplement in Nature, Science, or PNAS.
On a related note, Hugh complains that the reference year in which the curvilinear relationship between TFR and HDI is shown is a bad year to pick:
Also, it should be remembered, as I mention, we need to think about base years. 2005 was the mid point of a massive and unsustainable asset and construction boom. I think there is little doubt that if we took 2010 or 2011, the results would be rather different.
The problem with this is that the year is currently 2009, so we can't use data from 2010 or 2011. It seems entirely possible that the results would be different if we used 2011 data and I look forward to the paper in 2015 in which the Myrskylä hypothesis is re-evaluated using the latest demographic data. This is sort of the nature of social science research. There are very few Eureka! moments in social science. As I note above, we can't typically do the critical experiment that allows us to test a scientific hypothesis. Sometimes we can get clever with historical accidents (known in the biz as "natural experiments"). Sometimes we can use fancy statistical methods to approximate experimental control (such as the fixed effects estimation Myrskylä et al. use or the propensity score stratification used by Felton Earls and colleagues in their study of firearm exposure and violent behavior). If we waited until we had the perfect data to test a social science hypothesis, there would never be any social science. Perhaps things will indeed be different in 2011. If so, we may even get lucky and by comparing why things were different in 2005 and 2011, gain new insight into the relationships between human development and fertility. Until then, I am going to credit Myrskylä and colleagues for opening a new chapter on our understanding of fertility transitions.
Oh, and I plan to cite the paper, as I'm sure many other demographers will too...